|
Question 1138670: (144,108,81,60.75,...)
Is the sequence arithmetic, geometric, or neither?
-I said geometric
Write an expression for the nth term.
-I'm not sure what equation is supposed to be used. I'm pretty sure It's either:
-Sn=a1(1-r^n/1-r) or Sn=n(a1+an/2)
Calculate the first 10 terms. Express your answer to 5 places past the decimal.
-Would I used one of the formulas above and just plug in 1-10?
Does the sequence above have an infinite sum? If so, calculate the infinite sum. If not, tell why it does not have an infinite sum.
- Is infinite sum a different equation? I don't know what that is
Found 2 solutions by josgarithmetic, jim_thompson5910:
Answer by josgarithmetic(39616)   (Show Source):
Answer by jim_thompson5910(35256) (Show Source):
You can put this solution on YOUR website!
Is the sequence arithmetic, geometric, or neither?
You are correct in saying that the sequence is geometric. If you divide each term by its previous term, then you'll find that...
(term2)/(term1) = 108/144 = 0.75
(term3)/(term2) = 81/108 = 0.75
(term4)/(term3) = 60.75/81 = 0.75
Each time we get the same result, confirming we have a geomtric sequence. The common ratio is 0.75; telling us "multiply each term by 0.75 to get the next term"
For example
Start with 144 and multiply by 0.75 to get 144*0.75 = 108, which is the proper second term of the sequence.
===============================================================================================================
Write an expression for the nth term.
We have a = 144 as the first term and r = 0.75 as the common ratio; therefore, the nth term of the geometric sequence is:
Side note: Because  , we can write the nth term formula as 
===============================================================================================================
Calculate the first 10 terms. Express your answer to 5 places past the decimal.
There are two ways to do this:
1) We can multiply each term by 3/4 = 0.75 to generate the next term until we get to term ten
2) Plug in n = 1, 2, 3, ..., 9, 10 into the formula we got in the prior section
I'll go with option 2 since it will help confirm the answer in the prior section more
Plug in n = 1
 which is the proper first term
----------------------------
Plug in n = 2
 which is the proper second term
----------------------------
Plug in n = 3
 which is the proper third term
----------------------------
Plug in n = 4
 which is the proper fourth term
We have confirmed the four terms given to us.
----------------------------
Plug in n = 5
----------------------------
Plug in n = 6
 Rounding to five decimal places
----------------------------
Plug in n = 7
 Rounding to five decimal places
----------------------------
Plug in n = 8
 Rounding to five decimal places
----------------------------
Plug in n = 9
 Rounding to five decimal places
----------------------------
Plug in n = 10
 Rounding to five decimal places
----------------------------
The ten terms we get are
144
108
81
60.75
45.5625
34.17188
25.62891
19.22168
14.41626
10.81219
===============================================================================================================
Does the sequence above have an infinite sum? If so, calculate the infinite sum. If not, tell why it does not have an infinite sum.
Yes this sequence has an infinite sum. If you extend the terms out to infinity, and add them all up, then you'll approach some fixed finite number. This is because the terms steadily get smaller and smaller. Meaning that the approach to this fixed number, call it S for now, has a smaller step. If the terms got bigger and bigger, then there is no way to approach some finite fixed number and we would say the series diverged. Because this sequence has an infinite sum, we say that the infinite geometric series converges.
A formulaic way to know that this series converges is the fact that r = 0.75 is between r = -1 and r = 1. It makes the inequality  true. Your book may write 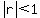 which is a compact way of saying
Plug a = 144 and r = 0.75 into the formula below and simplify
The infinite sum is 576.
Here is a table of partial sums to help show that we do approach 576 as n heads to infinity
Note: The  refers to the nth partial sum. It is found by adding the first n terms of the  sequence.
For instance, the 5th partial sum  happens when we add the first n = 5 terms, so,  which is shown in the n = 5 row and column.
|
|
|
| |
