SOLUTION: Hello, My question is 2x^4+15x^3+31x^2+20x+4 find all rational zeros of the polynomial, and then find the irrational zeros if any.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Hello, My question is 2x^4+15x^3+31x^2+20x+4 find all rational zeros of the polynomial, and then find the irrational zeros if any.      Log On


   

Question 1138616: Hello,
My question is
2x^4+15x^3+31x^2+20x+4 find all rational zeros of the polynomial, and then find the irrational zeros if any.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
Rational Roots Theorem tells you that your polynomial may have possible roots of the negatives of 1/2, 1, 2, 4. Those are the possible RATIONAL roots to check. (Use synthetic division to check each). Go from there.

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

The polynomial is   p(x) = 2x^4 + 15x^3 + 31x^2 + 20x + 4


The possible rational roots, based on the Rational Roots theorem, are


  (+/- 4/1) = +/- 4;   (+- 4/2) = +/- 2;  (+- 2/1) = +- 2;  (+- 2/2) = +- 1;  (+- 1/2).


The plot of the polynomial is shown in the Figure below.



    


    Plot y = 2x%5E4+%2B+15x%5E3+%2B+31x%5E2+%2B+20x+%2B+4


From the plot, is is clear that 


    -2 is very possible candidate;  

    -1%2F2 is a potential candidate; and 

     the root between -4 and -5 is an irrational number.


Immediate direct check/substitution proves that -2 is the root and -1%2F2 is the root, too.


Then the original polynomial is divisible by the product  (x+2)*(2x+1),  and long division gives the quotient


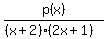    p%28x%29%2F%28%28x%2B2%29%2A%282x%2B1%29%29 = x^2 +5x +2.


Use the quadratic formula and find two remaining real irrational roots of the polynomial.

-------------

The lesson to learn from my post is THIS: 

    The Rational Root theorem is a good tool, but the analysis becomes much more quicker and productive, 

    if you use graphic calculator or plotting tool to visualize a polynomial.

    By doing in this way, you will be able to cut off easily the dead branches.