SOLUTION: A motorboat travels 70mi in 2 hours going upstream. It travels 90mi going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: A motorboat travels 70mi in 2 hours going upstream. It travels 90mi going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1138430: A motorboat travels 70mi in 2 hours going upstream. It travels 90mi going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of the current?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52865) About Me  (Show Source):
You can put this solution on YOUR website!
.
Against the current the effective speed (the speed relative to the river bank) is


u - v = 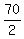70%2F2 = 35  miles per hour.     (1)   (u = the speed of the motorboat in still water;  v = the speed of the current)



With the current, the effective speed is

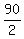u + v = 90%2F2 =  45 miles per hour.     (2)



Add equations (1) and (2)


2u = 35 + 45 = 80  ====>  u = 80/2 = 40 mph is the speed of the motorboat in still water.    ANSWER



Subtract eq(1) from eq(2)

2v = 45 - 35 = 10  ====>  v = 10/2 = 5 mph  is the speed of the current.     ANSWER

Solved.

The lesson to learn from this solution and the things to memorize are : 

    1.  The effective speed of a boat traveling with    a current is the sum        of the two speeds.

    2.  The effective speed of a boat traveling against a current is the difference of the two speeds.

    3.  It gives a system of two equations in two unknowns, which fits very well to be solved by the elimination method.


Answer by greenestamps(13206) About Me  (Show Source):
You can put this solution on YOUR website!


After determining that the upstream rate is 35mph and the downstream rate is 45mph, finish the problem quickly and easily with logical reasoning.

One of those rates is the speed of the boat in still water PLUS the speed of the current; the other is the speed of the boat in still water MINUS the speed of the current. Logical reasoning says the speed of the boat in still water has to be the rate halfway between those two rates.

So the speed of the boat in still water is (35+45)/2 = 40mph, which makes the speed of the current 5mph.