SOLUTION: There are 8 swimmers in a race. In how many ways can they finish if there are no dead heats and the swimmer in Lane 2 finished after the swimmer in Lane 5? I'm not quite sure ho

Algebra ->  Probability-and-statistics -> SOLUTION: There are 8 swimmers in a race. In how many ways can they finish if there are no dead heats and the swimmer in Lane 2 finished after the swimmer in Lane 5? I'm not quite sure ho      Log On


   

Question 1138418: There are 8 swimmers in a race. In how many ways can they finish if there are no dead heats and the swimmer in Lane 2 finished after the swimmer in Lane 5?
I'm not quite sure how to solve this. Any help would be appreciated
Answer by ikleyn(52794) About Me  (Show Source):
You can put this solution on YOUR website!
.

            This problem has unexpected and beautiful solution. 


The number of permutations where #2 goes before #5 is exactly equal to the number of permutations where #2 goes AFTER #5,


so each of these numbers is half of 8!, which is the total number of all permutations of 8 objects.


ANSWER.  3*4*5*6*7*8 = 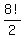8%21%2F2 = 20160 ways.