Question 1138315: 99.7% of the scores on an exam are between 60 and 98 points. Assuming the data is normally distributed, what are the mean and standard deviation?
Found 2 solutions by Boreal, Theo:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! 99.7% is +/- 3 sd
The mean is half the sum of 60 and 98 or 79
The difference between 60 and 79 and 79 and 98 is 19
each of those is 3 sd
so the sd is 19/3
N (69, 19/3)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! assuming the data is symmetric about the mean, you would do the following.
the mean would be halfway between 60 and 98.
take 98 - 60 to get 38 and divide that by 2 to get 19.
add 19 to 60 and the mean will be 79.
look up a z-scores that have .997 of the area under the normal distribution curve between them.
if the area between the z-scores is .997, that means the area outside this interval is 1 - .997 = .003.
divide that by 2 and the area to the right of the high z-score is .0015 and the area to the left of the low z-score is .0015.
if the area to the right of the high z-score is .0015, that means the area to the left of the high z-score is 1 - .0015 = .9985.
the z-score associated with an area of .9885 to the left of it is 2.967737927.
the z-score associated with an area of .0015 to the left of it is -2.967737927.
those are the z-scores that have .997 of the area under the normal distribution curve between them.
this can be seen in the following visual display.
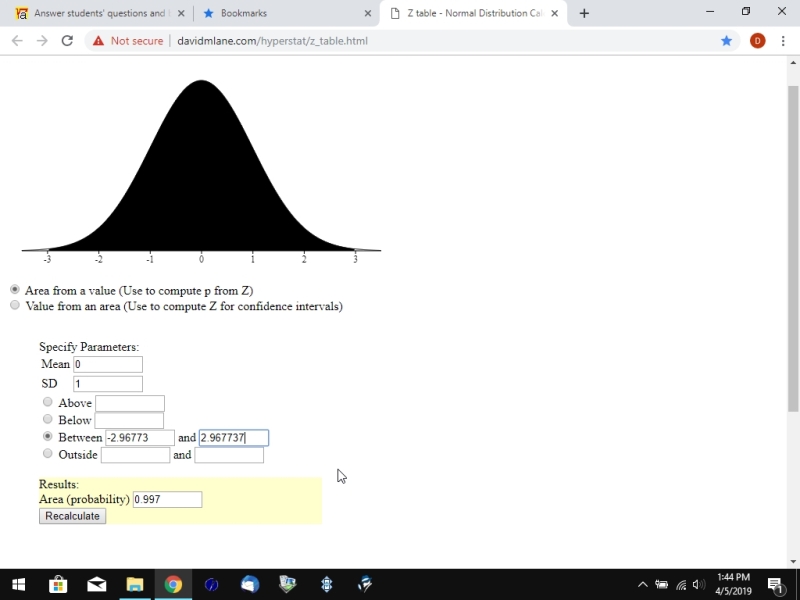
you would then use the z-score formula to find the standard deviation.
the z-score formula is z = (x - m) / s
z is the z-score
x is the raw score
m is the mean
s is the standard deviation
using the high side z-score, the formula becomes:
2.967737927 = (98 - 79) / s
solve for s to get s = 19 / 2.967737927 = 6.40218256.
that's the standard deviation.
that standard deviation applies to the high side z-score and the low size z-score because the normal distribution curve is symmetric about the mean.
to confirm, using the low side z-score the formula becomes:
-2.967737927 = (60 - 79) / s which becomes -2.967737927 = -19 / s.
solve for s to get s = -19 / -2.967737927 = the same as we got using the high side z-score.
you now have the mean and the standard deviation.
to confirm, use the online distributuion calculator, found at http://davidmlane.com/hyperstat/z_table.html
this is the same calculator i used above with z-scores, only this time i'm using it with raw scores.
when using with z-scores, the mean is 0 and the standard deviation is 1.
when using with raw scores, the mean is the mean of the distribution and the standard deviation is the standard deviation of the distribution.
the display from that calculator is shown below.

|
|
|