SOLUTION: 5. Determine the behavior of {{{f(x)=(2x^3-4x^2-16x)/(x^3-4x)}}} Domain : x – intercept(s) : Hole(s) : y – intercept : Vertical Asymptote(s) :

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: 5. Determine the behavior of {{{f(x)=(2x^3-4x^2-16x)/(x^3-4x)}}} Domain : x – intercept(s) : Hole(s) : y – intercept : Vertical Asymptote(s) :       Log On


   

Question 113820: 5. Determine the behavior of f%28x%29=%282x%5E3-4x%5E2-16x%29%2F%28x%5E3-4x%29
Domain :
x – intercept(s) :
Hole(s) :
y – intercept :
Vertical Asymptote(s) :
Horizontal Asymptote :

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Domain: Simply set the denominator equal to zero and solve for x

x%5E3-4x=0 Start with the given equation


x%28x%5E2-4%29=0 Factor out an x


x%28x%2B2%29%28x-2%29=0 Factor x%5E2-4 using the difference of squares


x=0, x%2B2=0, or x-2=0 Set each factor equal to zero


x=0, x=-2, or x=2 Solve for x in each case


Since x=0, x=-2, or x=2 makes the denominator zero, we must take these values out of the domain.


So our domain is:

which in plain English reads: x is the set of all real numbers except 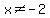x%3C%3E-2, x%3C%3E0, or x%3C%3E2





x-intercept(s): To find the x-intercepts, let f(x)=0 and solve for x

0=%282x%5E3-4x%5E2-16x%29%2F%28x%5E3-4x%29 Start with the given equation


2x%5E3-4x%5E2-16x=0 Set the numerator equal to zero. Remember the denominator cannot equal zero. So the numerator
can only equal zero.


2x%282x%5E2-4x-16%29=0 Factor out 2x


2x%28x-4%29%28x%2B2%29=0 Factor x%5E2-2x-8 to %28x-4%29%28x%2B2%29


2x=0, x-4=0, or x%2B2=0 Set each factor equal to zero


x=0, x=4, or x=-2 Solve for x in each case


So the possible x-intercepts are: x=0, x=4, or x=-2


However, since x=-2 and x=0 is not in the domain, the only x-intercept is x=4


Answer: The x-intercept is x=4




Holes:

f%28x%29=%282x%5E3-4x%5E2-16x%29%2F%28x%5E3-4x%29 Start with the given function


f%28x%29=x%282x%5E2-4x-16%29%2F%28x%28x%5E2-4%29%29 Factor out an x out of the denominator


f%28x%29=cross%28x%29%282x%5E2-4x-16%29%2F%28cross%28x%29%28x%5E2-4%29%29 Cancel like terms


f%28x%29=%282x%5E2-4x-16%29%2F%28x%5E2-4%29 Simplify



f%28x%29=%282%28x-4%29%28x%2B2%29%29%2F%28%28x-2%29%28x%2B2%29%29 Factor the numerator and denominator


f%28x%29=%282%28x-4%29cross%28%28x%2B2%29%29%29%2F%28%28x-2%29cross%28%28x%2B2%29%29%29 Cancel like terms


f%28x%29=%282%28x-4%29%29%2F%28x-2%29 Simplify


So here we can see that f%28x%29=%282%28x-4%29%29%2F%28x-2%29 is equivalent to f%28x%29=%282x%5E3-4x%5E2-16x%29%2F%28x%5E3-4x%29 . However, we must
keep in mind to exclude x=-2, x=0, and x=2 (remember the domain). Since we can plug in x=-2 and x=0 into
f%28x%29=%282%28x-4%29%29%2F%28x-2%29 (but not into f%28x%29=%282x%5E3-4x%5E2-16x%29%2F%28x%5E3-4x%29) we must make a mental note that there are holes
at x=-2 and x=0.


Answer: holes at x=-2 and x=0





y-intercept(s): To find the y-intercepts, let x=0 and solve for y


f%28x%29=%282%28x-4%29%29%2F%28x-2%29 Start with the simplified equation


f%28x%29=%282%280-4%29%29%2F%280-2%29 Plug in x=0


f%28x%29=%282%28-4%29%29%2F%28-2%29 Combine like terms


f%28x%29=%28-8%29%2F%28-2%29 Multiply


f%28x%29=4 Multiply


So when x=0, f(x) (which is y) is equal to 4.


Answer: So the y intercept is (0,4)




Vertical Asymptote(s):

Vertical asymptotes occur when the denominator is equal to zero. In other words, at the value of x that is not in the domain.

f%28x%29=%282%28x-4%29%29%2F%28x-2%29 Start with the simplified equation

x-2=0


x=2


Answer: So the vertical asymptote is x=2



Horizontal Asymptote(s):

To find the horizontal asymptote(s), simply take the leading coefficient of the numerator (which is 2) and divide it by the leading coefficient of the denominator (which is 1)


So simply divide 2 by 1 to get 2%2F1=2

So the horizontal asymptote is y=2



If we graph the function f%28x%29=%282x%5E3-4x%5E2-16x%29%2F%28x%5E3-4x%29, we can visually verify all of our answers:


Graph of f%28x%29=%282x%5E3-4x%5E2-16x%29%2F%28x%5E3-4x%29