Question 1138185: Joe is playing a game of chance at the hibiscus festival, costing $1 for each game. In the game two fair dice are rolled and the sum of the numbers that turned up is found. If the sum is seven, then Joe wins $5. Otherwise loses his money. Joe play the game 15 times. Find his expected profit or lose.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The probability of rolling a 7 is 1/6; the profit is -$1 + $5 = $4.
The probability of rolling any other sum is 5/6; the proft is -$1.
The expected profit for one game is

If he plays the game 15 times, his expected profit is

ANSWER: his expected profit playing the game 15 times is -$2.50 -- i.e., a loss of $2.50.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When two fair dice are rolled, there are 36 possible outcomes, each with the probability of  .
These outcomes are the pairs of integer numbers (i,j), where i and j take independently the values from 1 to 6.
The number of such pairs with the sum i+j = 7 is 6
( the pairs are (1,6), (2,5), (3,4), (4,3), (5,2) and (6,1) ).
So, the probability to get the sum of 7 at each roll of a pair of dice is .
These outcomes are the pairs of integer numbers (i,j), where i and j take independently the values from 1 to 6.
The number of such pairs with the sum i+j = 7 is 6
( the pairs are (1,6), (2,5), (3,4), (4,3), (5,2) and (6,1) ).
So, the probability to get the sum of 7 at each roll of a pair of dice is  = =  .
Mathematical expectation of the amount of money to win at each roll of a pair of dice is .
Mathematical expectation of the amount of money to win at each roll of a pair of dice is  dollars,
but Joe should pay one dollar for each roll,
so his expected profit at each roll of a pair of dice is dollars,
but Joe should pay one dollar for each roll,
so his expected profit at each roll of a pair of dice is
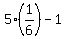 = = 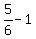 = = 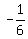 of a dollar.
Thus, statistically, Joe should expect the loss of a dollar.
Thus, statistically, Joe should expect the loss  of a dollar in each roll of a pair of dice.
Making 15 rolls in the game, Joe should expect to lose of a dollar in each roll of a pair of dice.
Making 15 rolls in the game, Joe should expect to lose 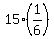 dollars = dollars =  dollars = $2.50. ANSWER dollars = $2.50. ANSWER
|
|
|