Question 1138080: Find the center, vertices, and foci of the ellipse with equation x squared divided by 144 plus y squared divided by 225 = 1. (5 points)
Center: (0, 0); Vertices: (0, -15), (0, 15); Foci: (-12, 0), (12, 0)
Center: (0, 0); Vertices: (0, -15), (0, 15); Foci: (0, -9), (0, 9)
Center: (0, 0); Vertices: (-15, 0), (15, 0); Foci: (0, -12), (0, 12) )
Center: (0, 0); Vertices: (-15, 0), (15, 0); Foci: (-9, 0), (9, 0)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the center, vertices, and foci of the ellipse with equation

compare to standard formula: 
so, your ellipse is centered at origin;  , ,
also,
 => =>
 => =>
 = distance to focus = distance to focus
For an ellipse with major axis parallel to the y-axis, the Foci (focus points ) are defined as :
( , , ), ( ), ( , ,  ), where ), where  is the distance from the center : ( is the distance from the center : ( , ,  ) to a focus ) to a focus




so, a focus will be at
( , , ), ( ), ( , , 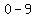 ) )
( , , ), ( ), ( , ,  ) )
the vertices are at ( , , ), ( ), ( , , 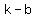 ) )
we have 
the vertices are at ( , ,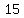 ), ( ), ( , ,  ) )
answer: Center: ( , ,  ); Vertices: ( ); Vertices: ( , ,  ), ( ), ( , ,  ); Foci: ( ); Foci: ( , ,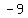 ), ( ), ( , ,  ) )
|
|
|