Question 1138077: Find the vertex, focus, directrix, and focal width of the parabola. choices below (5 points)
negative 1 divided by 16 times x squared = y
Vertex: (0, 0); Focus: (0, -4); Directrix: y = 4; Focal width: 16
Vertex: (0, 0); Focus: (-8, 0); Directrix: x = 4; Focal width: 64
Vertex: (0, 0); Focus: (0, 4); Directrix: y = -4; Focal width: 4
Vertex: (0, 0); Focus: (0, -4); Directrix: y = 4; Focal width: 64
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the vertex, focus, directrix, and focal width of the parabola. choices below

The standard form is  , where the focus is ( , where the focus is ( , ,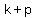 ) and the directrix is ) and the directrix is  . .
given:



=> , , =>the vertex at:( =>the vertex at:( , ,  ) )
 => =>
a focus at ( , , 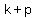 )=( )=( , ,  ) )
a directrix at  => =>
The focal width of a parabola is the length of a segment that is parallel to the directrix and passing through the focus of a parabola. The length of this segment is 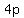 units, or four time the length from the focus to the vertex. units, or four time the length from the focus to the vertex.
focal width:
answer:Vertex: (0, 0); Focus: (0, -4); Directrix: y = 4; Focal width: 16
|
|
|