|
Question 113804: Find all the zeros of f (x) = 12x4 — 67x3 + 108x2 — 47x + 6
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! From part C), we found x=2 to be a zero for 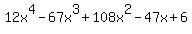 (ie f(2)=0) and the quotient was (ie f(2)=0) and the quotient was 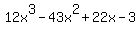 . So let's find the zeros for . So let's find the zeros for 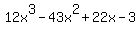
For 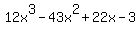 , the same sign rules apply as they do to the function , the same sign rules apply as they do to the function 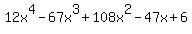 : there are no negative zeros and there are 4, 2, or no positive zeros : there are no negative zeros and there are 4, 2, or no positive zeros
So let's find the possible zeros for 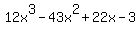
Any rational zero can be found through this equation
 where p and q are the factors of the last and first coefficients where p and q are the factors of the last and first coefficients
So let's list the factors of -3 (the last coefficient):

Now let's list the factors of 12 (the first coefficient):

Now let's divide each factor of the last coefficient by each factor of the first coefficient

Now simplify
These are all the distinct rational zeros of the function that could occur

To save time, I'm only going to use synthetic division on the possible positive zeros (using Descartes rule of signs) that are actually zeros of the function.
Otherwise, I would have to use synthetic division on every possible positive root (there are 12 possible positive roots, so that means there would be at most 12 synthetic division tables).
However, you might be required to follow this procedure, so this is why I'm showing you how to set up a problem like this
If you're not required to follow this procedure, simply use a graphing calculator to find the roots
So let's use the zero x=3 (which is an actual zero)
Now set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the numerator to the right of the test zero.
Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 12)
Multiply 3 by 12 and place the product (which is 36) right underneath the second coefficient (which is -43)
Add 36 and -43 to get -7. Place the sum right underneath 36.
Multiply 3 by -7 and place the product (which is -21) right underneath the third coefficient (which is 22)
Add -21 and 22 to get 1. Place the sum right underneath -21.
Multiply 3 by 1 and place the product (which is 3) right underneath the fourth coefficient (which is -3)
Add 3 and -3 to get 0. Place the sum right underneath 3.
Since the last column adds to zero, we have a remainder of zero. This means  is a factor of is a factor of 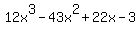
Now lets look at the bottom row of coefficients:
The first 3 coefficients (12,-7,1) form the quotient
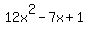
So 
You can use this online polynomial division calculator to check your work
Basically 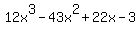 factors to factors to 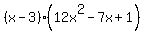
Now lets break 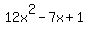 down further down further
 Set the expression equal to zero and solve for x Set the expression equal to zero and solve for x
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=12, b=-7, and c=1 Plug in a=12, b=-7, and c=1
 Negate -7 to get 7 Negate -7 to get 7
 Square -7 to get 49 (note: remember when you square -7, you must square the negative as well. This is because Square -7 to get 49 (note: remember when you square -7, you must square the negative as well. This is because  .) .)
 Multiply Multiply 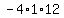 to get to get 
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 12 to get 24 Multiply 2 and 12 to get 24
So now the expression breaks down into two parts
 or or 
Lets look at the first part:

 Add the terms in the numerator Add the terms in the numerator
 Divide Divide
So one answer is

Now lets look at the second part:

 Subtract the terms in the numerator Subtract the terms in the numerator
 Divide Divide
So another answer is

So the solutions for 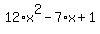 are: are:
 or or 
========================================================
Answer:
So the zeros are  , ,  , ,  , , 
|
|
|
| |