Question 1138026: The sides of an isosceles triangle have lengths of 10, 10, and 4. Find the measures of the base angles. Round your answers to the nearest tenth.
Show the equation used.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!

let the base angles be  and and  => =>
given:  , ,  , and , and 
let altitude to base  be be  , then sides , then sides  , , , and , and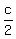 form right triangle where form right triangle where  is hypothenuse, is hypothenuse,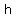 and and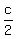 legs legs
since  and and  , we have , we have



using the sine rule:



 ° °
then
 ° °
and third angle  °=> °=> °=> °=> ° °
or, you can do it using the cosine rule:
 , ,  , and , and







 ° => ° =>  ° °
|
|
|