Question 1137928: A plane travels at a speed of 175mph in still air. Flying with a tailwind, the plane is clocked over a distance of 1000 miles. Flying against a headwind, it takes 1 hour longer to complete the return trip. What was the wind velocity?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let w be the wind velocity (in miles per hour).
Then the plane' speed with the wind is (175 + w) miles per hour,
and the time to fly 1000 miles with the wind is  hours.
Also, the plane' speed against the wind is (175 - w) miles per hour,
and the time to fly 1000 miles against the wind is hours.
Also, the plane' speed against the wind is (175 - w) miles per hour,
and the time to fly 1000 miles against the wind is 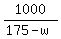 hours.
Now you can write the "time" equation hours.
Now you can write the "time" equation
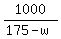 - -  = 1 hour
saying that "it takes 1 hour longer to complete the return trip".
It is your basic equation. To solve it, multiply both sides by (175+w)*(175-w). You will get
1000(175+w) - 1000(175-w) = 175^2 - w^2, or
2*1000*w = 175^2 - w^2
w^2 + 2000w - 175^2 = 0 = 1 hour
saying that "it takes 1 hour longer to complete the return trip".
It is your basic equation. To solve it, multiply both sides by (175+w)*(175-w). You will get
1000(175+w) - 1000(175-w) = 175^2 - w^2, or
2*1000*w = 175^2 - w^2
w^2 + 2000w - 175^2 = 0
 = = 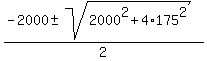 = =  .
Only positive value of the roots is meaningful: w = .
Only positive value of the roots is meaningful: w = 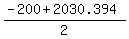 = 15.197.
ANSWER. The wind' speed is 15.197 miles per hour.
CHECK. = 15.197.
ANSWER. The wind' speed is 15.197 miles per hour.
CHECK. 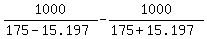 = 1 hour. ! Correct ! = 1 hour. ! Correct !
Solved, answered, checked and completed.
---------------------
It is a typical "tailwind and headwind" word problem.
See the lessons
- Wind and Current problems
- Wind and Current problems solvable by quadratic equations
- Selected problems from the archive on a plane flying with and against the wind
in this site, where you will find other similar solved problems with detailed explanations.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! r * t = d
r = rate
t = time
d = distance
plane flies at 175 mph.
distance = 1000 miles.
plane flies with the wind in one direction and against the wind in the other direction.
it takes t hours with the wind and t + 1 hour against the wind.
w = the speed of the wind.
with the wind, the formula becomes (175 + w) * t = 1000
against the wind, the formula becomes (175 - w) * (t + 1) = 1000
since they're both equal to 1000, you get:
(175 + w) * t = (175 - w) * (t + 1)
simplify each side of this equation t0 get:
175 * t + w * t = 175 * t + 175 - w * t - w
subtract 175 * t from both sides of the equation to get:
w * t = 175 - w * t - w
add w * t to both sides of the equation to get:
2 * w * t = 175 - w
add w to both sides of the equation to get:
2 * w * t + w = 175
factor out the w to get:
w * (2t + 1) = 175
solve for w to get:
w = 175 / (2t + 1)
simplify the first equation of (175 + w) * t = 1000 to get:
175 * t + w * t = 1000
replace w with 175 / (2t + 1) to get:
175 * t + 175 / (2t + 1) * t = 1000
multiply both sides of this equation by (2t + 1) to get:
175 * t * (2t + 1) + 175 * t = 1000 * (2t + 1)
simplify further to get:
350 * t^2 + 175 * t + 175 * t = 2000 * t + 1000
combine like terms to get:
350 * t^2 + 350 * t = 2000 * t + 1000
subtract 2000 * t and subtract 1000 from both sides of the equation to get:
350 * t^2 - 1650 * t - 1000 = 0
factor this quadratic equation to get:
t = 5.257705786321 or t = -0.54342007203528
t can't be negative, so t = 5.257705786321
replace t in the first equation with 5.257705786321 to get:
(175 + w) * t = 1000 becomes (175 + w) * 5.257705786321 = 1000
simplify this equation to get 920.098512606 + 5.257705786321 * w = 1000
solve for w to get:
w = (1000 - 920.098512606) / 5.257705786321 = 15.197025212
you have:
t = 5.257705786321
w = 15.197025212
(175 + w) * t = 1000 becomes (175 + 15.197025212) * 5.257705786321 = 1000 which becomes 1000 = 1000 which is true.
(175 - w) * (t + 1) = 1000 becomes (175 - 15.197025212) * (5.257705786321 + 1) = 1000 which becomes 1000 = 1000 which is true.
solution is confirmed to be good.
your solution is that the velocity of the wind is 15.197025212 miles per hour in the original direction of the trip.
|
|
|