Question 1137781: Heron's Formula Word Problem:
Help, please! I am verey stuck on this difficult problem.
Heron's formula gives a method of finding the area of a triangle if the lengths of its sides are known. Suppose that a, b, and c are the lengths of the sides. Let s denote one-half of the perimeter of the triangle (called the semiperimeter), that is, s=1/2(a+b+c). Then the area of the triangle is
A=s(s−a)(s−b)(s−c). Find the area of an island in the form of a triangle if the sides of this triangle measure approximately 16 mi, 10 mi, and 8 mi.
______mi squared
Found 3 solutions by greenestamps, ikleyn, Theo:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Heron's formula LOOKS difficult; but with a little practice it is quite easy to use... although the resulting arithmetic can be rather ugly.
Note you have not stated the formula correctly. The area is NOT s(s-a)(s-b)(s-c); it is the SQUARE ROOT OF s(s-a)(s-b)(s-c).
Let's use the formula to find the area of this triangular island.
s = (1/2)(a+b+c)
This defines the semiperimeter s of the triangle -- one-half of the sum of the lengths of the three sides. The first step in using Heron's formula is to determine this number.
In your example, the perimeter is 16+10+8 = 34; so the semiperimeter is 34/2 = 17.
A=sqrt(s(s−a)(s−b)(s−c))
This looks ugly; but, again, it is easy to use, with a little practice. The formula tells you that, to find the area, you first multiply 4 numbers together: the semiperimeter s, and the semiperimeter minus each of the individual side lengths (s-a), (s-b), and (s-c).
In your problem, s is 17, and the side lengths are 16, 10, and 8. So the 4 numbers you multiply together are s=17, s-a = 17-16 = 1, s-b = 17-10 = 7, and s-c = 17-8 = 9. The product is
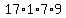
Then the area is the square root of that number:

Here is another example where the numbers are "nicer": find the area of a triangle with side lengths 6, 8, and 10.
You might recognize this as a right triangle with legs 6 and 8; its area using the familiar formula one-half base times height is (6*8)/2 = 24. Let's find that result using Heron's formuls.
s = (6+8+10)/2 = 12
s-a = 12-6=6
s-b = 12-8=4
s-c = 12-10=2
sqrt(s(s-a)(s-b)(s-c)) = sqrt(12*6*4*2) = sqrt(12*12*4) = 12*2 = 24
Answer by ikleyn(52855)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the formula is:
A = sqrt(s * (s - a) * (s - b) * (s - c))
your formula omitted th square root of all those goodies.
s = (a + b + c) / 2.
this is the perimeter of the triangle divided by 2.
in your problem, s = (16 + 10 + 8) / 2 = 34/2 = 17
the formula for area becomes A = sqrt(17 * (17 - 16) * (17 - 10) * (17 - 8)).
this becomes A = sqrt(17 * 1 * 7 * 9) which becomes A = sqrt(1071) which becomes A = 32.72613634.
i checked with an online heron's formula calculator and confirmed this is the correct answer.
the heron's formula calculator can be found at http://www.csgnetwork.com/herontriangleareacalc.html
here's a display of the results of using that calculator.


|
|
|