SOLUTION: determine the coefficient of x^9 y^4 in the binomial expansion of (x + y)^13 power

Click here to see ALL problems on Binomial-probability

Question 1137744: determine the coefficient of x^9 y^4 in the binomial expansion of (x + y)^13 power
Found 3 solutions by MathLover1, MathTherapy, greenestamps:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!

+...
=>

the coefficient of in the binomial expansion of power is

Answer by MathTherapy(10555)   (Show Source):
You can put this solution on YOUR website!

determine the coefficient of x^9 y^4 in the binomial expansion of (x + y)^13 power

In the BINOMIAL EXPANSION of 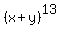, x⁹y⁹ occurs at the term where:
As such, 9 = 13 - (r - 1) OR 4 = r - 1
9 = 13 - r + 1 5 = r
9 - 14 = - r
- 5 = - r
5 = r
With the coefficients on x and y in 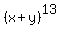being 1, the coefficient on the 5th term, when expanded, will be the value in the 5th COLUMN of the 13th ROW of Pascal’s triangle, which is
OR
With the coefficient on x and y being 1, the coefficient on the 5th term will be:
FYI: The entire EXPANSION DOESN'T HAVE to be done, as one person decided to do!
What if was the 24th or 25th term of the expansion? Do you think it'd be wise to do the entire expansion? Think about it!

Answer by greenestamps(13203)   (Show Source):
You can put this solution on YOUR website!

Since the coefficients of x and y are both 1, the coefficient of the x^9y^4 term in the expansion of (x+y)^13 is