SOLUTION: find all real and imaginary roots x^4+3x^3+x^2+4=0

find all real and imaginary roots



Possible rational roots, if it has any,
are ±1,±2,±4

DesCartes rule of signs tells us that
there are no positive roots, so that
narrows down the possible rational
roots to -1, -2, and -4

Try , or 

So we try dividing synthetically 
by . But we must first put in a
zero term since the original
equation does not contain a term
in x.  So we rewrite the original
equation, showing all coefficients: 



-1|1  3  1  0  4
  |  -1 -2  1 -1
   1  2 -1  1  3

So we see that we don't get 0 as a
remainder, the bottom right number,
but rather 3, so -1 is not a root.

So we try  to see if it is a root.
Dividing synthetically by  

-2|1  3  1  0  4
  |  -2 -2  2 -4
   1  1 -1  2  0

So  is a root, since we get 0
as a remainder.  The 4 numbers to the
left of the zero represent the quotient
when we divided by , so we have now
factored the polynomial equation as





So we now try to find a rational root of



DesCartes rule of signs tells us this
has possible roots ±1 and ±2.  But since
the original equation has no positive roots
this can only have rational roots -1 and -2.
We know -1 is not a root because it was not
a root of the original equation, so we can
only try  again as a root of multiplicity
2.   is equivalent to . so we
divide the new polynomial also by :

-2| 1  1 -1  2
  |   -2  2 -2
    1 -1  1  0

Yes, we get 0 as a remainder, so  is
a root of multiplicity 2. So now our
factorization of the original polynomial
is now:





We set each factor = 0,

 gives root 
 gives root , again


This does not factor, so must be solved by the 
quadratic formula:

Its roots are 



or, simplifying:







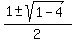
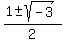
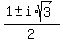So there are four roots, counting multiplicities
of roots as though they were separate roots:

, , , 


Edwin