Prove by induction that for all positive integers value of n:
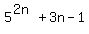 is an integer multiple of 9.
is an integer multiple of 9.
First we show that it is true when n=1:
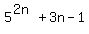
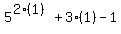
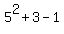
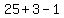
 , which is a multiple of 9 since 9∙3 = 27
Now we show that IF it were true when n=k, that it would also be true
when n=k+1.
We let a multiple of 9 be 9P where P is an integer such that
when n=k,
, which is a multiple of 9 since 9∙3 = 27
Now we show that IF it were true when n=k, that it would also be true
when n=k+1.
We let a multiple of 9 be 9P where P is an integer such that
when n=k, 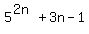 equals to 9P. That is, we examine
what would happen IF this were true for some value of k:
equals to 9P. That is, we examine
what would happen IF this were true for some value of k:
 we hope (but do not know!) that if that were true, then when we substitute
(k+1) for n, like this:
we hope (but do not know!) that if that were true, then when we substitute
(k+1) for n, like this:
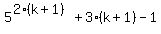 that it will be a multiple of 9 also, so we simplify it:
that it will be a multiple of 9 also, so we simplify it:
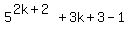
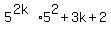
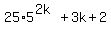 We notice that the first term is 25 times the first term of
We notice that the first term is 25 times the first term of 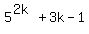 ,
so we see what we must add to 25 times
,
so we see what we must add to 25 times 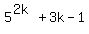 to get
to get 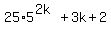 .
25 times
.
25 times 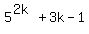 is
is 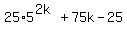 . So we write
. So we write
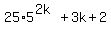 as
as
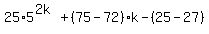 which is
which is
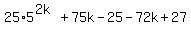 , which is
, which is
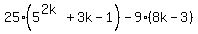 , which is
, which is
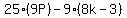 , which is
, which is
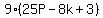 , which is a multiple of 9.
Now since we have a value of n, namely k=1, for which
, which is a multiple of 9.
Now since we have a value of n, namely k=1, for which
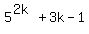 is a multiple of 9, then we have
proved that we also have another value of n, namely k+1 or 1+1 or
2 for which
is a multiple of 9, then we have
proved that we also have another value of n, namely k+1 or 1+1 or
2 for which 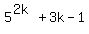 is a multiple of 9.
Now since we have a value of n, namely k=2, for which
is a multiple of 9.
Now since we have a value of n, namely k=2, for which
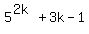 is a multiple of 9, then we have
proved that we also have another value of n, namely k+1 or 2+1 or
3 for which
is a multiple of 9, then we have
proved that we also have another value of n, namely k+1 or 2+1 or
3 for which 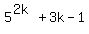 is a multiple of 9.
Now since we have a value of n, namely k=3, for which
is a multiple of 9.
Now since we have a value of n, namely k=3, for which
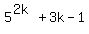 is a multiple of 9, then we have
proved that we also have another value of n, namely k+1 or 3+1 or
4 for which
is a multiple of 9, then we have
proved that we also have another value of n, namely k+1 or 3+1 or
4 for which 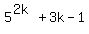 is a multiple of 9.
And so on and on for all positive integer values of n.
Edwin
is a multiple of 9.
And so on and on for all positive integer values of n.
Edwin