|
Question 1137650: Determine the coordinates of the orthocentre of triangle DEF with vertices at D (-3,4) E (8,-2) F (4,5)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
given: 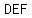 with vertices at with vertices at
 ( ( , , ) )
 ( ( , , ) )
 ( ( , , ) )
the orthocenter: the point where the three "altitudes" of a triangle meet
find the slopes of the lines that contain segments  and and
slope of 
now, we need a slope of perpendicular line, altitude to segments  : :
slope of perpendicular line, altitude :  -> -> 
 (substitute (substitute  , ,  , ,  ) )





equation of the altitude to  : :

slope of 
altitude to  : :  -> -> 
 (substitute (substitute  , ,  , ,  ) )




equation of the altitude to  : :

intersection of the altitudes will be orthocenter
equation 1: 
equation 2: 
Solving for  and and  : :








The coordinates are (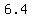 , ,  ). This is the orthocenter. ). This is the orthocenter.

|
|
|
| |