Question 1137551: A real estate manages 80 apartment units. When the rent of each unit is $180 per month, all units are occupied. However, for each $6 increase in rent, one of the units becomes vacant. Each occupied unit requires an average of $18 per month for service and repairs. Show that $336 or $342 should be charged to realise the most profit.
Answer by ikleyn(52769)   (Show Source):
You can put this solution on YOUR website! .
From the condition, when the rent price is 180 + 6i, where i is the number of the 6-dollar increments,
the number of units occupied is
N(i) = 80 - i.
So, the revenue is R(i) = (180+6i)*N(i) = (180+6i)*(80-i).
But the profit, which is the major targeted goal to maximize, is
P(i) = (180 + 6i - 18)*(80-i) = (162+6i)*(80-i) = -6i^2 + 318i + 162*80.
We want to find " i " to maximize this quadratic function of " i ".
From the general theory, i =  =  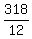= 26.5.
The closest integers are i= 26 and i= 27, which give the optimal renting price
180 + 6i = 180 + 6*26 = 336 dollars or 180 + 6*27 = 342 dollars.
Solved.
----------------------
On finding the maximum/minimum of a quadratic function see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
/\/\/\/\/\/\/\/\/
To see other similar solved problems, look into the lesson
- Using quadratic functions to solve problems on maximizing revenue/profit
in this site (from the same textbook).
|
|
|
