Question 1137528: A farmer bought 3 seeds. The probability of each of them germinating is 3/5. If he plants all of them,find the probability that only one of them germinate.
Found 2 solutions by Boreal, jim_thompson5910:
Answer by Boreal(15235)   (Show Source): (Show Source):
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We have three seeds which we'll label as A,B,C
seed A has a germinating probability of 3/5 = 0.6, so it has a failure probability of 1-0.6 = 0.4; the same can be said for the other two seeds (B and C)
Let's consider three scenarios:
Scenario 1: Seed A germinates, the other two seeds do not germinate. Since each seed's event is independent of one another, we multiply the probability values to get 0.6*0.4*0.4 = 0.096, so the probability of scenario 1 happening is 0.096
Scenario 2: Seed B germinates, the other two seeds do not germinate. This is effectively the same as scenario 1 above. So we ge the same probability as before, which is 0.096
Scenario 3: Seed C germinates, the other two seeds do not germinate. Like with the previous scenario, we get the same probability.
Scenarios 1 through 3 are mutually exclusive events. If one scenario happens, then the other scenarios cannot happen. There is no overlap. Or put another way, no two scenarios can happen at the same time. Because the mutually exclusive events, we can add the probabilities:
0.096+0.096+0.096 = 0.288
--------------------------------------------------------------
An alternative is to use the binomial probability formula
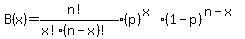
where,
n = 3 is the number of trials or seeds
x = 1 is the count we want to germinate
p = 3/5 = 0.6 is the chance of germination for any one seed
The exclamation marks mean factorial notation
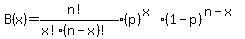






We get the same answer 0.288
side note: the decimal value 0.288 converts to the fraction 288/1000 = 36/125
|
|
|