SOLUTION: Which value of k does the following system of equations have a non trivial solution (k-4)x + x² = 0 x + (k-4)x² = 0

(k-4)x +      x^2 = 0     (1)

x      + (k-4)x^2 = 0     (2)



Let assume that x=/= 0 and reduce factor x in both sides of both equations (1) and (2). You will get


(k-4) +      x   = 0      (3)

1     + (k-4)x   = 0      (4)


From equation (3),  x = - (k-4).   Substitute it i to equation (4). You will get


1 + (k-4)*(-(k-4)) = 0,    or

(k-4)^2 = 1,

k - 4  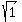=  = +/- 1.


Thus we should consider two cases.


a)  k - 4 = 1  ====>  k = 1 + 4 = 5.


    Then the system (1), (2) takes the form

        x + x^2 = 0     (5)

        x + x^2 = 0     (6).


    Thus the system (1),(2) in this case becomes the system of two identical equations (5) and (6);

    in other words, it becomes one single equation

        x + x^2 = 0,

    which is equivalent to  x*(x+1) = 0  and has non-trivial (non-zero) solution x = -1.



b)  k - 4 = -1  ====>  k = -1 + 4 = 3.


    Then the system (1), (2) takes the form

        -x + x^2 = 0     (7)

        x  - x^2 = 0     (8).


    In this case the system (1),(2)  becomes the system of two identical equations (7) and (8);

    in other words, it becomes one single equation

        x - x^2 = 0,

    which is equivalent to  x*(x-1) = 0 and has non-trivial (non-zero) solution x = 1.


Answer.  For two values k = 5  and  k = 3,  the system (1),(2) has non-trivial solutions  x= -1  and  x= 1, respectively.