Question 1137449: do the diagonals of ABCD bisect each other?
A(-1,-7), B(-3,-5), C(-2,2), D(0,0)
There is nothing in my notes on this and I emailed my teacher asking for help. So any help is appreciated. Thanks!
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The diagonals of quadrilateral ABCD bisect each other if and only if the midpoints of diagonals AC and BD are the same point.
Use the given coordinates to find the midpoints of AC and BD to find the answer to the problem.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a quadrilateral is a 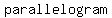 , then the diagonals , then the diagonals 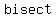 each other. each other.
If  || ||  , ,  || ||  , it’s a parallelogram. Parallel lines have , it’s a parallelogram. Parallel lines have 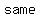 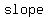 . .
So, if slope of  = to slope of = to slope of  , and slope of , and slope of  = to slope of = to slope of  then it’s a then it’s a 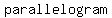 . .
slope of  is is 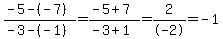
slope of  is is 
=>slope of  is same is same
slope of 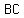 is is
slope of  is is 
=>slope of and  is same is same
hence,  || ||  , ,  || ||  ,=> ,=> 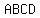 is a is a 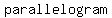
that is enough to prove the diagonals of 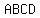 bisect each other bisect each other
you can also do it this way:
find midpoint  of diagonals of diagonals  and and  , prove that distances , prove that distances  and and 
| Solved by pluggable solver: Finding midpoint of 2 points |
We use the midpoint formula to solve. The x coordinate is  Plug in the values, Plug in the values,
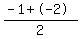  The x coordinate is -1.5. Now for the y. The x coordinate is -1.5. Now for the y.
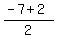  The y coordinate is -2.5. The midpoint is at point (-1.5,-2.5). The y coordinate is -2.5. The midpoint is at point (-1.5,-2.5).
|
midpoint of diagonal AC:is at point (-1.5,-2.5)
The distance 
The distance 
| Solved by pluggable solver: Finding midpoint of 2 points |
We use the midpoint formula to solve. The x coordinate is  Plug in the values, Plug in the values,
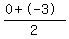  The x coordinate is -1.5. Now for the y. The x coordinate is -1.5. Now for the y.
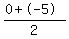  The y coordinate is -2.5. The midpoint is at point (-1.5,-2.5). The y coordinate is -2.5. The midpoint is at point (-1.5,-2.5).
|
midpoint of diagonal BD: is at point (-1.5,-2.5)
The distance 
The distance 
check the graph:

so, answer is: the diagonals of 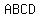 bisect each other bisect each other
|
|
|