Question 1137365: It was not, thank you for catching that! Here it is A kayak can travel 30 miles downstream in 5 hours, while it would take 15 hours to make the same trip upstream. Find the speed of the kayak in still water, as well as the speed of the current. Let k represent the speed of the kayak in still water, and let c represent the speed of the current.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52835)   (Show Source):
You can put this solution on YOUR website! .
The speed of the kayak downstream,  = 6 miles per hour, is the sum k + c.
The speed of the kayak upstream, 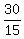 = 2 miles per hour, is the difference k - c.
So, you have these two equations
k + c = 6, (1) and
k - c = 2 (2)
Add the equation to eliminate "c" and to get
2k = 6 + 2 = 8, k = 8/2 = 4 miles per hour.
Then from equation (1), c = 6 - k = 6 - 4 = 2.
Answer. Kayak speed in still water is 4 mph. The speed of the current is 2 mph.
CHECK. Check the solution by your own, by substituting the found value into the condition.
Solved, explained and completed.
-------------------
It is a typical and standard Upstream and Downstream round trip word problem.
You can find many similar fully solved problems on upstream and downstream round trips with detailed solutions in lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Wind and Current problems solvable by quadratic equations
- Unpowered raft floating downstream along a river
- Selected problems from the archive on the boat floating Upstream and Downstream
in this site, where you will find other similar solved problems with detailed explanations.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
The given distance and the given times tell you the upstream speed is 2mph and the downstream speed is 6mph. Algebraically, with k for the speed of the kayak in still water and c for the speed of the current, that can be represented by
k+c = 6
k-c = 2
Then you can solve the problem using formal algebra using those two equations.
But this is an example of a wide variety of problems in which you get to a point where the information lets you find the sum and difference of two numbers. In that kind of problem, you can finish the problem easily by some simple logical reasoning.
Think of the sum and difference of the two numbers on a number line. You start at one of the numbers; if you add the second number, you end up one place, and if you subtract the second number, you end up at a second place. Since you went the same distance in each direction to get to those two ending places, the place you started has to be halfway between those two ending places.
So given that the sum of two numbers is A and the difference is B, the first number is halfway between A and B.
In this problem, the sum of the kayak's speed and the river's speed is 6mph; the difference is 2mph. That means the kayak's speed is halfway between 6mph and 2pmh, which is 4mph, and that makes the speed of the current 2mph.
So to solve this problem, once you have the upstream and downstream speeds of 2mph and 6mph, you can immediately conclude that the kayak's speed is 4mph and the speed of the current is 2mph.
Here is another common type of problem that uses the same simple solution method.
The sum of two numbers is 25; their difference is 11. Find the two numbers.
You can quickly reason that one number is halfway between 25 and 11, which is 18; then the other number must be 7.
|
|
|
