|
Question 1137268: Find the inverse of matrix of elements cos theta - sin theta
sin theta cos theta
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Check out this article to see how to find the inverse of a 2x2 matrix.
Part of the steps will have us compute the determinant. The determinant of the 2x2 matrix is found through this formula
E = determinant
E = a*d - b*c
where a,b,c,d are arranged like this in the matrix

In this case,
a = cos(theta)
b = -sin(theta)
c = sin(theta)
d = cos(theta)
which we can see through this comparison
 & -\sin(\theta)\\\sin(\theta) & \cos(\theta)\end{bmatrix})
So the determinant is,
E = a*d - b*c
E = cos(theta)*cos(theta) - (-sin(theta))*sin(theta)
E = cos(theta)*cos(theta) + sin(theta)*sin(theta)
E = cos^2(theta) + sin^2(theta)
E = 1
For that last step, you use the pythagorean trig identity.
Therefore, the expression 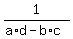 is equal to 1 is equal to 1  , meaning that this portion does not affect the result. This is because multiplying by 1 does not change the answer. We can ignore this piece because the determinant is 1. , meaning that this portion does not affect the result. This is because multiplying by 1 does not change the answer. We can ignore this piece because the determinant is 1.
In that same article I posted, note how the original matrix looks like this

and it becomes this

You swap a and d; also change the signs of b and c but keep them in the same spot.
Since
a = cos(theta)
b = -sin(theta)
c = sin(theta)
d = cos(theta)
we can say...
 & -(-\sin(\theta))\\-\sin(\theta) & \cos(\theta)\end{bmatrix})
 & \sin(\theta)\\-\sin(\theta) & \cos(\theta)\end{bmatrix})
which is the inverse of the original matrix. I'll let you confirm this by computing A*B and B*A, where A is the original matrix and B is the inverse matrix. You should get AB = I and BA = I. Recall that the matrix I is the identity matrix.
|
|
|
| |