Question 1137264: Things did not go quite as planned. You invested $21,020, part of it in a stock that paid 12% annual interest. However, the rest of the money suffered a 5% loss. If the total annual income from both investments was $2026, how much was invested at each rate?
Answer by ikleyn(52790)   (Show Source):
You can put this solution on YOUR website! .
Let x = amount invested at 12%, in dollars.
Then the second amount, which suffered the 5% loss, is the rest (21020-x) dollars.
The interest from the 12% interest amount is 0.12*x dollars.
The 5% loss from the second amount is 0.05*(21020-x) dollars.
Your equation is
interest - loss = final interest, or
0.12*x - 0.05*(21020-x) = 2026 dollars.
From the equation, express x and calculate the answer
x = 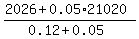 = 18100.
Answer. The amount at 12% is $18100; the rest $21020-$18100 = $2920 is the amount suffered 5% loss.
Check. 0.12*18100 - 0.05*2920 = 2026 dollars. ! Correct !
-----------------
It is a typical and standard problem on investment.
To see many other similar solved problems on investment, look into the lesson
- Using systems of equations to solve problems on investment
in this site.
You will find there different approaches (using one equation or a system of two equations in two unknowns), as well as
different methods of solution to the equations (Substitution, Elimination).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
