Question 1137237: The following set of points belong to a specific function:{(1,-6),(2,-6),(-2,0),(0,-5),(-1,-3)}. Based on the set of points answer the following questions:
a) What type of function does the set of points produce? Justify your answer.
b) Write the equation for this function based on the set of points that have been given.
- I plotted the points on a graph and joined them with a line but I don't know if that's the right thing to do. It kinda throws me off to have the first 2 points right beside each othe and suggests not a smooth curve. (Or something??) I really done even know what else to do at all and we didn't learn anything like this in the unit that we are doing in Advanced Functions!
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are many ways you could go about determining a function whose graph contains the given points. But I have no idea what you have and have not studied to this point.
So I will go ahead and describe what I did to find the answer and see if it makes sense to you, based on what you have studied.
With the five plotted points, walking along the graph from left to right, the graph gets less and less steep, and between the last two points the graph is flat. The decreasing slope suggests a quadratic function (parabolic graph). The fact that the function values are the same at x=1 and x=2 also could indicate a parabola, since a parabola has an axis of symmetry.
So let's guess that, with the function values the same at x=1 and x=2, the function is a parabola with an axis of symmetry at x = 1.5 (halfway between x=1 and x=2).
Next, using the symmetry of a parabola, we know one root is at x=-2, because (-2,0) is a point on the graph. With a root at x=-2 and an axis of symmetry at x = 1.5, the other root is at x=5.
Then the equation is

To determine the value of a, use the known y-intercept (0,-5):
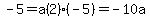

The equation of the parabola is

Now, at this point we don't KNOW that this is the equation we want; we need to show that the coordinates of ALL the given points satisfy this equation. It turns out that they do; so we have the correct equation.
ANSWERS: The function is a quadratic polynomial with equation 
|
|
|