Question 1136921: A baseball team plays in a stadium that holds 68000 spectators. With the ticket price at $11 the average attendance has been 28000. When the price dropped to $9, the average attendance rose to 34000. Assume that attendance is linearly related to ticket price.
What ticket price would maximize revenue?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! when the price is 11, the attendance is 28000.
when the price is 9, the attendance is 34000.
when the price drops by 2 dollars, the attendance goes up by 6000.
since this is linear, the slope intercept form of the equation would be y = mx + b.
m is the slope and b is the y-intercept.
the slope is (y2 - y1) / (x2 - x1).
(x1,y1) = (11,28000)
(x2,y2) = (9,34000)
the slope is (y2 - y1) / (x2 - x1) = (34000 - 28000) / (9 - 11) = 6000 / -2 = -3000.
y = mx + b becomes y = -3000 * x + b
solve for b by replacing x and y with one of the points.
i chose (9,34000).
y = -3000 * x + b becomes 34000 = -3000 * 9 + b
solve for b to get b = 34000 + 27000 = 61000
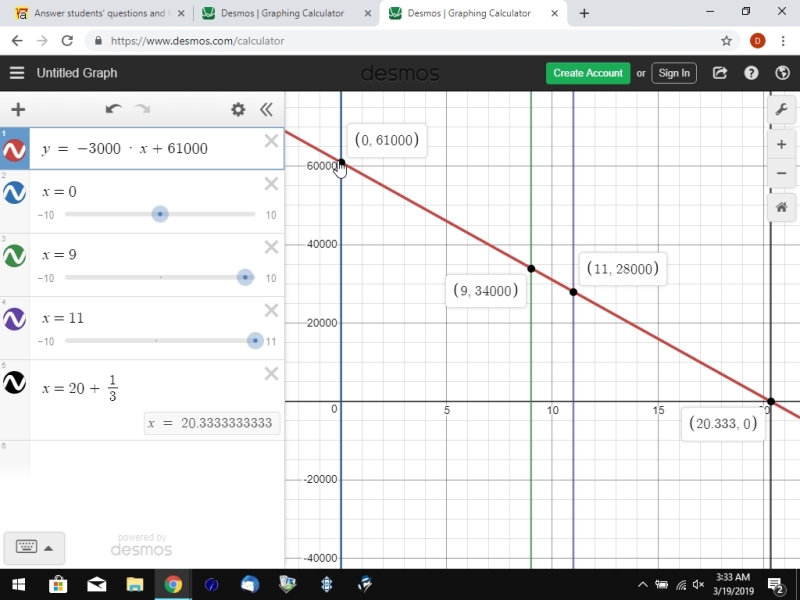
the slope intercept form of the equation for the price is y = -3000 * x + 61000.
this equation can be graphed and is shown below.
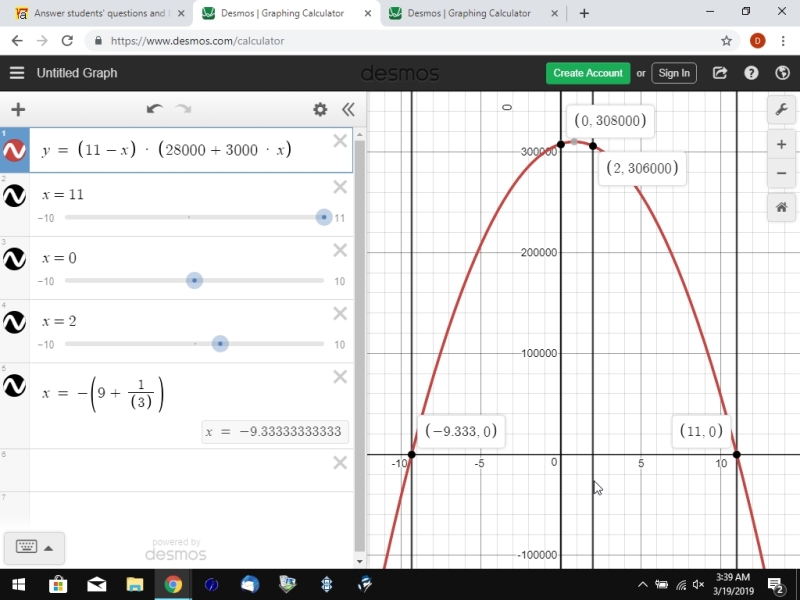
the revenue equation is y = (11 - x) * (28000 + 3000 * x)
that equation can be graphed and is shown below.
the revenue equation is a quadratic equation.
the standard form of that equation is y = -3000 * x^2 + 5000 * x + 308000.
in standard form, you get a = -3000, b = 5000, c = 308000.
the maximum revenue occurs when x = -b / 2a.
that becomes -5000 / -6000 = 5 / 6 = .8333333333.....
when x = .833333....., price = 11 - .8333333 = 10.666666666 and quantity becomes 28000 + 3000 * .8333333 = 30500.
since revenue = price * quantity, revenue = 10.166666666... * 30500 = 310083.33333333....
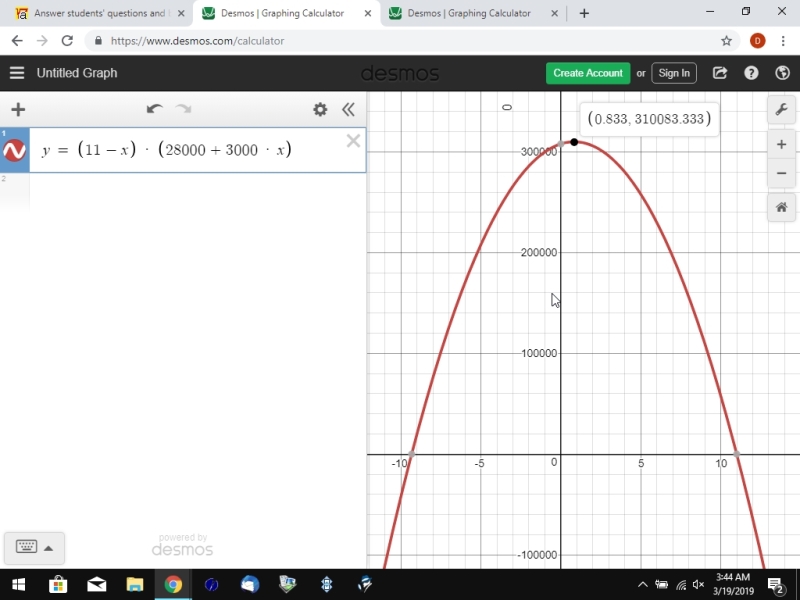
the maximum revenue can be seen on the following graph.
you have two basic equations associated with this problem.
the first equation is y = -3000 * x + 61000.
in this equation, x is the price and y is the quantity of tickets sold.
when the price is 0, you can sell 61000 tickets.
notice that the capacity is 68000, so you won't fill up the stadium even if you give the tickets away, based on this equation.
when the price is 20 and 1/3 per ticket. you will sell none based on this equation.
when the price is 11, you sell 28000.
when the price is 9, you sell 34000.
the second equation is y = (11 - x) * (28000 + 3000 * x)
in this equation, y is the revenue and x is the change in the price and 3000 * x is the change in the quantity for each change in the price.
when x = 0, the price is 11 and the quantity is 28000 and the revenue is 11 * 28000 = 308000.
when x = 2, the price is 9 and the quantity is 34000 and the revenue is 9 * 34000 = 306000.
when x is 11, the price is 0 and the quantity is 61000 and the revenue is 0 * 61000 = 0.
when x is -9.333333333, the price is 20.33333333 and the quantity is 0 and the revenue = 0.
the same revenue graph also shows when the maximum revenue occurs.
that occurs when x = .8333333333.
the price is 11 - .8333333333 = 10.1666666666... and the quantity is 28000 + .8333333333 * 3000 = 30500 and the revenue is 10.166666..... * 30500 = 310083.33333.....
the maximum revenue is shown on the last graph.
it's the same as the second graph except only the maximum revenue is shown for clarity.
note that the equation shown on the revenue graph is y = (11 - x) * (28000 + 3000 * x).
this is the same equation as y = -3000 * x^2 + 5000 * x +308000.
those two equations are equivalent to each other, just shown in different forms.
|
|
|