Question 1136757: Solve the equation x^4-13x^2+30?
List all real solutions, separated by commas?
x=
Found 3 solutions by Boreal, Alan3354, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website!
this factors into an x^2- and an x^2- because the middle term is negative and last term is positive. One can use a u substitution where u=x^2
(u-10)(u+3)=0 The given is an expression, the equal sign 0 makes it an equation.
u=10 and -3
x^2=10
x+=/- sqrt (10) or (-sqrt(10), + sqrt (10)) ANSWER.
The other two solutions are complex/imaginary
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! That is not an equation.
Equations have equal signs.
---
x^4-13x^2+30 = 1 is an equation.
x^4-13x^2+30 = 5 is an equation.
x^4-13x^2+30 = 100 is an equation.
Answer by ikleyn(52812)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
First, it is not an equation, since it has no right side and the equality sign.
So, we can talk about a polynomial, but not about equation.
And the question, if to formulate it correctly, should be THIS :
Find the roots of this polynomial.
Second, the solution and the answer by @Boreal both are incorrect, since his factoring is incorrect.
Below find the correct solution.
Introduce new variable u = x^2.
Then your polynomial takes the form
u^2 - 13u + 30
It can be factored in this way
u^2 - 13u + 30 = (u-3)*(u-10)
so, it has the roots u = 3 and u = 10, both positive.
It means, that the original polynomial has 4 (four) real roots  , ,  , ,  and and 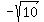 . ANSWER . ANSWER
Solved.
|
|
|