Question 1136612: Sarah left Minneapolis heading east on the interstate at a speed of 60 mph. Her sister followed her on the same route, leaving three hours later and driving at a rate of 75 mph. How long, in hours, will it take for Sarah's sister to catch up to Sarah?
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Sarah left Minneapolis heading east on the interstate at a speed of 60 mph. Her sister followed her on the same route, leaving three hours later and driving at a rate of 75 mph. How long, in hours, will it take for Sarah's sister to catch up to Sarah?
2 hours, as suggested by someone is WRONG!!! For the sister to take 2 hours, she'd have to be traveling @ 150 mph.
Isn't that dangerous and illegal? They're not on a racetrack, I'm sure, just the interstate! Not even on the AUTOBAHN can they go that fast!
Even that's VERY HIGH speed on the AUTOBAHN (average speed: 150 km/h or 80 mph)
I hope you realized this and have IGNORED that answer!
Correct answer: 12 hours!
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will present you 3 ways to solve this problem.
1. The way on how physicists do it
When the sister started, Sarah was 3 hours * 60 mph = 180 miles ahead.
Bur the sister moved faster, decreasing the distance between them by 15 = 75 - 60 miles each hour.
So, the sister will catch Sarah in 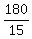 = 12 hours. ANSWER = 12 hours. ANSWER
2. Formal algebra solution. It is a way how beginner algebra students do it.
Let " t " be the time (in hours) for Sarah's sister to catch up to Sarah.
During this time, Sarah' sister will cover the distance of 75*t miles.
Sarah moved in her car (t+3) hours and covered 60*(t+3) miles.
At the catching moment, these two distances are the same.
It gives you an equation
75t = 60*(t+3).
It your basic equation to find t. Simplify and solve it:
75t = 60t + 180
75t - 60t = 180
15t = 180 ===============> t = 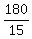 = 12.
You get the same answer 12 hours, as in the previous solution. = 12.
You get the same answer 12 hours, as in the previous solution.
3. The way on how experienced students do it.
Experienced student is the student who solved such problems 5 - 10 times.
He writes this fraction
time to catch up =  = = 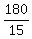 = 12 hours
and obtains the answer in one line.
Notice that the numerator of the fraction is the "head start distance" for Sarah,
while the denominator is the difference of the speeds, which is the relative speed.
Experienced student keeps all these explanations in his (or her) mind, and has no need to repeat it again and again. = 12 hours
and obtains the answer in one line.
Notice that the numerator of the fraction is the "head start distance" for Sarah,
while the denominator is the difference of the speeds, which is the relative speed.
Experienced student keeps all these explanations in his (or her) mind, and has no need to repeat it again and again.
-----------------
Congratulations ! Now you are familiar with 3 most applicable ways to solve "catching up" problems.
For introductory lessons on Travel and Distance problems see
- Travel and Distance problems
- Travel and Distance problems for two bodies moving in opposite directions
- Travel and Distance problems for two bodies moving in the same direction (catching up)
in this site.
They are written specially for you.
You will find the solutions of many similar problems there.
Read them and learn once and for all from these lessons on how to solve simple Travel and Distance problems.
Become an expert in this area.
/\/\/\/\/\/\/\/\/
I think there is no need to explain you that the "solution" by @josgarithmetic is totally wrong.
For your safety, simply ignore it.
|
|
|