SOLUTION: Let X and Y represent discrete random variables with {{{f(x,y)=(xy/18)}}} for x ∈ {1,2,3} and y ∈ {1,2}. Compute P(X = 1 and Y = 2) and P(X +Y = 4).

Algebra ->  Probability-and-statistics -> SOLUTION: Let X and Y represent discrete random variables with {{{f(x,y)=(xy/18)}}} for x ∈ {1,2,3} and y ∈ {1,2}. Compute P(X = 1 and Y = 2) and P(X +Y = 4).      Log On


   

Question 1136603: Let X and Y represent discrete random variables with f%28x%2Cy%29=%28xy%2F18%29 for x ∈ {1,2,3} and y ∈ {1,2}. Compute P(X = 1 and Y = 2) and P(X +Y = 4).
Answer by ikleyn(52925) About Me  (Show Source):
You can put this solution on YOUR website!
.

See how I edited your post to make sense : 

    Let X and Y represent discrete random variables with probability density function f%28x%2Cy%29=%28xy%2F18%29 for x ∈ {1,2,3} and y ∈ {1,2}. 

    Compute P(X = 1 and Y = 2) and P(X +Y = 4).

Without this editing the post MAKES NO SENSE.


Solution 

(a)  P(X = 1 and Y = 2) = f(1,2) = 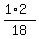%281%2A2%29%2F18 = 2%2F18 = 1%2F9.    ANSWER



(b)  Notice that  X + Y = 4 is possible only if  (X=3 AND Y=1)  OR  (X=2 AND Y=2).

     Therefore,

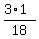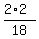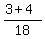     P(X + Y = 4) = P(X=3 AND Y=1) + P(X=2 AND Y=2) = f(3,1) + f(2,2) = %283%2A1%29%2F18 + %282%2A2%29%2F18 = %283%2B4%29%2F18 = 7%2F18.    ANSWER

Solved.