SOLUTION: Find the solutions of the equation that are in the interval [0, 2π). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.) sin 2t + sin t =

Algebra ->  Trigonometry-basics -> SOLUTION: Find the solutions of the equation that are in the interval [0, 2π). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.) sin 2t + sin t =       Log On


   

Question 1136559: Find the solutions of the equation that are in the interval [0, 2π). (Enter your answers as a comma-separated list. If there is no solution, enter NO SOLUTION.)
sin 2t + sin t = 0
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

sin+%282t+%29%2B+sin%28+t%29+=+0 , in the interval [0, 2pi)

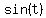
Use the following identity : sin+%282t%29=2+cos%28t%29sin%28t%29

2cos%28t%29sin%28t%29%2B+sin%28+t%29+=+0........factor out +sin%28+t%29

sin%28+t%29%282cos%28t%29+%2B+1%29+=+0

Solving each part separately:

sin%28+t%29+=+0 => in the interval [0, 2pi) for t=0, t=+pi , t=2pi

or
%282cos%28t%29+%2B+1%29+=+0=> in the interval [0, 2pi) for t=2pi%2F3, +t=4pi%2F3


Combine all the solutions:
t=0, t=+pi , t=2pi, t=2pi%2F3, +t=4pi%2F3