|
Question 1136546: A person invested $7200 for 1 year, part at 6%, part at 10%, and the remainder at 13%.
The total annual income from these investments was $787.
The amount of money invested at 13% was $200 more than the amounts invested at 6%
and 10% combined. Find the amount invested at each rate.
The person invested $[ ] at 6%,
$[ ] at 10%, and $[ ] at 13%.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52798)   (Show Source):
You can put this solution on YOUR website! .
The solution is in 3 steps.
1. One part of the condition says that the total amount is $7200.
The other part of the condition says that the amount invested at 13% is 200 more than the combined amount invested at 6% and 10%.
It implies immediately via simple logic, that the combined amount invested at 6% and 10% is 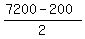 = 3500 dollars
and the amount invested at 13% is 3500+200 = 3700 dollars.
2. It implies that the interest produced by the amount at 13% is
0.13*3700 = 481 dollars
and the combined interest of two other accounts is 787 - 481 = 306 dollars.
3. Let x be the amount invested at 10%.
Then the amount invested at 6% is ((3500-x) dollars.
The combined interest equation for these two accounts is
0.10*x + 0.06*(3500-x) = 306.
The solution to this equation is
x = 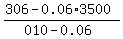 = 2400.
Answer. $3700 invested at 13%; $2400 invested at 10%, and (3500-2400) = 1100 dollars invested at 6%.
CHECK. 0.13*3700 + 0.10*2400 + 0.06*1100 = 787 dollars as the total interest. ! Correct !
Solved.
----------------
I'd like to make couple of comments to this solution.
The method of solution was to reduce the problem from 3 unknowns to only two unknowns.
Then the problem for two unknown investments was solved using single equation for only one unknown.
The method of reducing such problems from 3 unknowns to only two is very well known.
See the lesson
- HOW TO algebreze and solve this problem on 2 equations in 2 unknowns
in this site.
On solution of investment problems for two accounts see the lesson
- Using systems of equations to solve problems on investment
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
/\/\/\/\/\/\/\/\/
If you think that I hid from you the reducing step from 3 unknowns to 2 unknowns,
then I will present this step here EXPLICITLY.
Let A be the amount invested at 13% and B be the combined amount invested ar 6% and 10%.
We are given that
A + B = 7200
A - B = 200
---------------------- Add these two equations. You will get
2A = 7400 ==============> A = 7400/2 = 3700 dollars.
Then B = 7200 - 3700 = 3500 dollars, exactly as I stated in the core text.
Using logical arguments, take off $200 from $7200 - then you will get a total of $7000, consisting of two equal parts "reduced A" and "B",
so "B" is 7000/2 = 3500 dollars and "A" is 3500+200 = 3700.
Thus, now you have all the parts of the solution "in place".
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
(1) Use logical reasoning and simple mental arithmetic, or formal algebra, to determine from the given information that $3700 was invested at 13% and $3500 was split between the 6% and 10% investments.
(2) Find the income from the 13% investment:
$481 of the total income was from the investment at 13%.
(3) Determine the combined income from the 6% and 10% investments:
The total income from the 6% and 10% investments was $306.
(4) Now here is a completely different method for determining how the $3500 was split between the 6% and 10% investments.
All $3500 at 6% would produce income of $210; all at 10% would produce income of $350.
The ratio in which the $3500 is split between the 6% and 10% investments is exactly determined by where the actual income lies between $210 and $350.
350-210 = 140; 306-210 = 96; 96/140 = 24/35.
$306 is 24/35 of the way from $210 to $350; this means 24/35 of the $3500 was invested at the higher rate.
24/35 of $3500 = $2400 at 10%; the rest, $1100, at 6%.
ANSWERS: $3700 at 13%; $2400 at 10%; $1100 at 6%.
|
|
|
| |
