Question 1136543: 2.24 Exit poll: Edison Research gathered exit poll results from several sources for the Wisconsin recall election of Scott Walker. They found that 53% of the respondents voted in favor of Scott Walker. Additionally, they estimated that of those who did vote in favor for Scott Walker, 37% had a college degree, while 44% of those who voted against Scott Walker had a college degree. Suppose we randomly sampled a person who participated in the exit poll and found that he had a college degree. What is the probability that he voted in favor of Scott Walker?
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In order for the problem COULD BE SOLVED, we need to introduce an additional assumption,
that all voters who not voted for Scott Walker, voted against him.
Then the solution is as follows:
Voted for SW Voted against SW
53% 47%
Of them, Of them,
with a college degree with a college degree
37% 44%
Now the formula and the value for the probability under the question is/are
P = 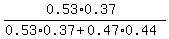 = 0.4867 = 48.67%. ANSWER = 0.4867 = 48.67%. ANSWER
This formula is self-explanatory. If you need additional explanations,
look into this formula, and it will tell you everything about itself.
----------------
To see many other similar solved problems, look into the lesson
- Advanced probability problems from the archive
in this site.
Look also into this link
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1136116.html
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1136116.html
where you will find the solution to similar problem in the archive to this forum, which I solved several days ago.
|
|
|