SOLUTION: Find the center, vertices, and foci of the ellipse with equation 2x2 + 9y2 = 18. choices below A.Center: (0, 0); Vertices: (0, -3), (0, 3); Foci: Ordered pair zero comma nega

Algebra ->  Trigonometry-basics -> SOLUTION: Find the center, vertices, and foci of the ellipse with equation 2x2 + 9y2 = 18. choices below A.Center: (0, 0); Vertices: (0, -3), (0, 3); Foci: Ordered pair zero comma nega      Log On


   

Question 1136090: Find the center, vertices, and foci of the ellipse with equation 2x2 + 9y2 = 18.
choices below

A.Center: (0, 0); Vertices: (0, -3), (0, 3); Foci: Ordered pair zero comma negative square root seven and ordered pair zero comma square root seven

B.Center: (0, 0); Vertices: (0, -9), (0, 9); Foci: Ordered pair zero comma negative square root seventy seven and ordered pair zero comma square root seventy seven

C.Center: (0, 0); Vertices: (-9, 0), (9, 0); Foci: Ordered pair negative square root seventy seven comma zero and ordered pair square root seventy seven comma zero

D.Center: (0, 0); Vertices: (-3, 0), (3, 0); Foci: Ordered pair negative square root seven comma zero and ordered pair square root seven comma zero
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Find the center, vertices, and foci of the ellipse with equation
2x%5E2+%2B+9y%5E2+=+18........both sides divide by 18
2x%5E2%2F18+%2B+9y%5E2%2F18+=+18%2F18
x%5E2%2F9+%2B+y%5E2%2F2+=1
=> h=0, k=0,a=sqrt%289%29=±3, b=sqrt%282%29
center:(0,0)

c=sqrt%289-2%29=sqrt%287%29

the vertices are at (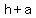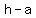h%2Ba,k), (h-a, k )
(0%2B3,0)=(3,0)
(0-3,0)=(-3,0)
(h%2Bc,k), (h-c, k )
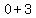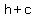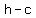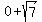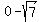(0%2Bsqrt%287%29,0)= (sqrt%287%29,0)
(0-sqrt%287%29, k )=(-sqrt%287%29,0)



answer:
D.Center: (0, 0); Vertices: (-3, 0), (3, 0); Foci: Ordered pair negative square root seven comma zero and ordered pair square root seven comma zero