Question 1136030: Phyllis invested 43000dollars, a portion earning a simple interest rate of 5
percent per year and the rest earning a rate of 7
percent per year. After one year the total interest earned on these investments was 2430 dollars. How much money did she invest at each rate?
At rate 5percent :
At rate 7percent :
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
I will show you two methods of solving this problem.
Solution 1. Using the system of 2 equations
Let x be the amount invested at 5% and y be the amount invested at 7%.
Then you have these two equations
x + y = 43000 dollars (1) (the sum of amounts is equal to the total investment)
0.05x + 0.07y = 2430 dollars (2) (the sum of interests is equal to the total interest)
I will apply the Substitution method to solve the system.
For it, I express
x = 43000 - y (3)
from the first equation and then substitute it into the second equation, replacing x. I will get
0.05*(43000 - y) + 0.07y = 2430. (4)
Simplify and solve this equation step by step:
0.05*43000 - 0.05y + 0.07y = 2430
0.07y - 0.05y = 2430 - 0.05*43000
0.02y = 280
y = 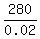 = 14000.
Thus we found that $14000 were invested at 7%.
To find x, use equation (3)
x = 43000 - 14000 = 29000.
ANSWER. $29000 invested at 5% and $14000 invested at 7%.
CHECK. 0.05*29000 + 0.07*14000 = 2430 dollars, the total interest. ! Correct !
Solution 2. Using single equation
Let y be the amount invested at 7%.
Then the amount invested at 5% is the rest (43000-y) dollars.
The 5% investment gives the interest of 0.05*(43000-y) dollars.
The 7% investment gives the interest of 0.07*y dollars.
In total, these two investments give $2430. Therefore, the "interest" equation is
0.05*(43000-y) + 0.07*y = 2430.
It is the same equation (4) as you obtained in the Solution 1 after substitution.
So, the solution of this equation is the same, and it produces the same answer.
My solutions and explanations are completed.
You learned two methods setuping the equations along with the methods of their solutions.
H a p p y l e a r n i n g !
--------------------
It is a standard and typical problem on investments.
If you need more details, or if you want to see other similar problems solved by different methods, look into the lesson
- Using systems of equations to solve problems on investment
in this site.
You will find there different approaches (using one equation or a system of two equations in two unknowns), as well as
different methods of solution to the equations (Substitution, Elimination).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is a completely different method without algebra which, if you understand how to use it, can get you to the answer to a problem like this much faster and with far less effort than traditional algebraic methods.
This is essentially a mixture problem -- you are mixing investments at 5% and 7% and receiving an overall percentage return somewhere between 5% and 7%.
The key to this method of solving mixture problems is that the ratio in which the total investment is split exactly determines where the overall percentage lies between the 5% and 7%.
$43,000 all at 5% would yield $2150 interest.
$43,000 all at 7% would yield $3010 interest.
Find where the actual interest of $2430 lies between $2150 and $3010:
3010-2150 = 860; 2430-2150 = 280; 280/860 = 28/86 = 14/43
Those simple calculations show that $2430 is 14/43 of the way from $2150 to $3010; that means 14/43 of the total investment was at the higher rate.
ANSWER: 14/43 of $43,000, or $14,000, at 7%; the rest, $29,000, at 5%.
CHECK: .07(14000)+.05(29000) = 980+1450 = 1430
|
|
|
