Question 1135976: Find the vertex, focus, directrix, and focal width of the parabola.
x2 = 20y
choices are below
Vertex: (0, 0); Focus: (0, 5); Directrix: y = -5; Focal width: 20
Vertex: (0, 0); Focus: (5, 0); Directrix: x = 5; Focal width: 5
Vertex: (0, 0); Focus: (5, 0); Directrix: y = 5; Focal width: 80
Vertex: (0, 0); Focus: (0, -5); Directrix: x = -5; Focal width: 80
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
 is the standard equation for a right-left facing parabola with vertex at ( ,  )
rewrite in the standard form :
 .........factor 
 ....simplify
rewrite as
so, (, )= ( , ), 
parabola is symmetric around the y-axis and so the focus lies a distance  from the center (, ) along the y-axi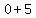s
(, )
(, )
(, )->focus
the distance between the focus and directrix is 
parabola is symmetric around the y-axis and so the directrix is a line parallel to the x-axis, a distance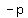 from the center left (,) x-coordinate
the focal width is 
answer:
Vertex: (, ); Focus: (, ); Directrix:  ; Focal width: 
Answer by greenestamps(13209)  (Show Source):
You can put this solution on YOUR website!
For me, the most useful form of the equation of a parabola (that opens up or down) is
In this form...
(1) the vertex is (h,k);
(2) p is the (directed) distance from the vertex to the focus; which means -p is the directed distance from the vertex to the directrix; and
(3) 4p is the focal width (length of the latus rectum)
Written in that form, the equation in your example is
So...
(1) the vertex is (0,0);
(2) 4p=20 so p=5, so the focus is (0,5) and the directrix is y = -5; and
(3) the focal width is 4p = 20
The first answer choice is the correct one.
|
|
|
