.
Let x =  .
Then
.
Then  =
=  =
=  =
= 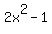 .
Therefore, the given equation
.
Therefore, the given equation 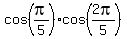 =
=  takes the form
takes the form
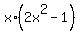 =
=  , or, equivalently
, or, equivalently
 = 0.
The roots of the polynomial
= 0.
The roots of the polynomial  are:
are:
 =
=  , (1)
, (1)
 =
= 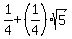 (2)
(2)
 =
= 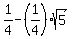 (3)
Explanation
This is a polynomial of degree 3. To find zeros for polynomials of degree 3 or higher we use Rational Root Test.
The Rational Root Theorem tells you that if the polynomial has a rational zero then it must be a fraction
(3)
Explanation
This is a polynomial of degree 3. To find zeros for polynomials of degree 3 or higher we use Rational Root Test.
The Rational Root Theorem tells you that if the polynomial has a rational zero then it must be a fraction  ,
where p is a factor of the trailing constant and q is a factor of the leading coefficient.
The factors of the leading coefficient (8) are 1, 2, 4, 8 . The factor of the constant term (-1) is 1 .
Then the Rational Roots Tests yields the following possible solutions:
± 1/1, ±1/2, ±1/4, ±1/8 .
Substitute the POSSIBLE roots one by one into the polynomial to find the actual roots. Start first with the whole numbers.
If we plug these values into the polynomial P(x), we obtain
,
where p is a factor of the trailing constant and q is a factor of the leading coefficient.
The factors of the leading coefficient (8) are 1, 2, 4, 8 . The factor of the constant term (-1) is 1 .
Then the Rational Roots Tests yields the following possible solutions:
± 1/1, ±1/2, ±1/4, ±1/8 .
Substitute the POSSIBLE roots one by one into the polynomial to find the actual roots. Start first with the whole numbers.
If we plug these values into the polynomial P(x), we obtain 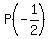 = 0.
To find remaining zeros we use Factor Theorem. This theorem states that if
= 0.
To find remaining zeros we use Factor Theorem. This theorem states that if  is root of the polynomial
then this polynomial can be divided with qx−p. In this example:
Divide P(x) with 2x+1
is root of the polynomial
then this polynomial can be divided with qx−p. In this example:
Divide P(x) with 2x+1
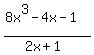 =
= 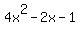 .
Polynomial
.
Polynomial 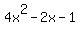 can be used to find the remaining roots.
can be used to find the remaining roots.
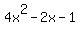 is a second degree polynomial. To find its roots use the quadratic formula.
is a second degree polynomial. To find its roots use the quadratic formula.
FINAL
Of the found roots (1), (2) and (3), only positive root (2) can be the value of x =  .
Therefore,
.
Therefore,  =
= 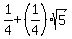 . ANSWER
. ANSWER
Solved.