Question 1135842: The sum of three terms of an A.P. is 21 and the product of the first and third exceeds the second term by 6, find the terms.
Found 4 solutions by MathLover1, Boreal, ikleyn, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the three terms of AP are  , ,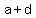 , ,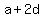 . .
Now,
As per the question ,



=> => =>  ....eq.1 ....eq.1
Now,


 .........substitute .........substitute  from eq.1 from eq.1



 ...factor ...factor




so you will get
 , or , or 
find 
 ....eq.1 ....eq.1


or
 ....eq.1 ....eq.1


Now, there will be two AP:
 , , , ,  and and  , , , ,
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! a1+a2+a3=21
note, a2 is n more than a1 and a3 is n more than a2 so the sum is 3a2=21 and a2=7
a1*a3=a2+6
so a1*a3=13
a2-a1=a3-a2
a1=1
a2=7
a3=13
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the middle term  .
Then .
Then  = x - d, = x - d,  = x + d.
Also, = x + d.
Also,  + +  + +  = (x-d) + x + (x+d) = 3x,
therefore the first statement of the condition means that
3x = 21, which implies x = = (x-d) + x + (x+d) = 3x,
therefore the first statement of the condition means that
3x = 21, which implies x =  = 21/3 = 7.
The second statement of the condition means then that = 21/3 = 7.
The second statement of the condition means then that
 . . = (7-d)*(7+d) = 7 + 6 = 13, or = (7-d)*(7+d) = 7 + 6 = 13, or
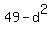 = 13 ====> = 13 ====>  = 49 - 13 = 36 ====> d = = 49 - 13 = 36 ====> d = 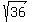 = +/- 6.
So, the three terms of the progression are EITHER
7 - 6 = 1, 7, 7 + 6 = 13
OR in reverse order
13, 7, 1. = +/- 6.
So, the three terms of the progression are EITHER
7 - 6 = 1, 7, 7 + 6 = 13
OR in reverse order
13, 7, 1.
Solved.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a quick informal solution, if an algebraic solution is not required.
The middle term in an AP with three terms is the average of the terms. If the sum of the three terms is 21, then the middle term is 7.
The given information then says the product of the first and third terms is 7+6=13. Since 13 = 1*13, the first and last terms are (in either order) 1 and 13.
ANSWERS: 1, 7, 13 or 13, 7, 1
|
|
|