SOLUTION: You want to be able to withdraw $45,000 from your account each year for 25 years after you retire. You expect to retire in 30 years. If your account earns 9% interest, how

    You want to be able to withdraw $45,000 from your account at the beginning of each year for 25 years after you retire. 

    You expect to retire in 30 years. 

    If your account earns 9% interest compounded yearly, how much will you need to deposit at the end of each year 
    until retirement to achieve your retirement goals?

Step 1 is to determine what amount you need to have at your account after 30 years depositing to it

in order for to be able to withdraw $45,000 from your account at the beginning of each year for 25 years after you retire.


The general formula to calculate this amount is  

    X = .

In this case  the withdrawal semi-annual rate is W = $45000,  the annual compounding rate 
is  r = 0.09,  p = 1 + 0.09 = 1.09, the number of payment periods  is n = 25. So


    X = 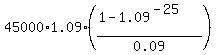 = 481,797.53 dollars.     

At this step we determine how big the annual deposit should be to provide this amount of $481,797.53 after 30 years of depositing.


This time it is classic Ordinary Annuity saving plan.  The general formula is 


    FV = ,   


where  FV is the future value of the account;  P is annual payment (deposit); r is the annual percentage yield presented as a decimal; 
n is the number of deposits (= the number of years, in this case).


From this formula, you get for the annual payment 


    P = .     (1)


Under the given conditions, FV = $481,797.53;  r = 0.09;  n = 30.  So, according to the formula (1), you get for the annual payment 


    P = 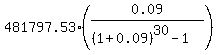 = $3534.64.


So, your annual deposit should be  $3534.64.     ANSWER


ANSWER.  To provide your goal, you need to deposit  $3534.64 dollars annually at the end of each year during 30 years.