Question 1135573: For the function f(x) = |x2 - 3| - 2x, find the values of x such that f(x) = 0
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solving absolute value equation is very important part of your mathematical education in the school.
Therefore, ignore writing by @josgarithmetic and listen and read me attentively.
You have an equation
|x^2 -3| - 2x = 0. (1)
The major idea, strategy and methodology is to divide the entire number line in parts, where the function
under the absolute value remains positive or negative and then, based on the definition of the absolute value, take off
the absolute value signs and simplify the given equation in this way.
Then we solve the simplified equation associated with each partial interval, find the root / (the roots) and check
(notice, it is VERY important part of the solution) if the found root belongs to the current partial interval.
Now let's look how it works for the given equation.
1. The quadratic binomial (x^2 - 3) is negative over the interval  < x < < x <  .
Therefore, in this interval, |x^2-3| = -(x^2-3), and the original equation take the form
-(x^2 - 3) - 2x = 0. (2)
Simplify and solve it
x^2 + 2x - 3 = 0 (2') ====> .
Therefore, in this interval, |x^2-3| = -(x^2-3), and the original equation take the form
-(x^2 - 3) - 2x = 0. (2)
Simplify and solve it
x^2 + 2x - 3 = 0 (2') ====>
 = = 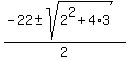 = = 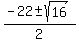 = = 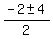 .
So, the equation (2') has two roots .
So, the equation (2') has two roots  = = 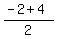 = 1 and = 1 and  = =  = -3.
Of these two roots, the root = -3.
Of these two roots, the root  = 1 lies in the interval ( = 1 lies in the interval ( , , )
THEREFORE, it is also the root of the original equation (1).
From the other side, the root )
THEREFORE, it is also the root of the original equation (1).
From the other side, the root  = -3 doe not belong to the interval ( = -3 doe not belong to the interval ( , , )
THEREFORE, it does not follow from our consideration that the root of )
THEREFORE, it does not follow from our consideration that the root of  = -3 is the root of the original equation (1).
At this point, we completed our consideration of the interval ( = -3 is the root of the original equation (1).
At this point, we completed our consideration of the interval ( , , ).
2. The quadratic binomial (x^2 - 3) is positive outside the interval ).
2. The quadratic binomial (x^2 - 3) is positive outside the interval  < x < < x <  .
This outside part, as you understand, consists of two semi-infinite intervals
( .
This outside part, as you understand, consists of two semi-infinite intervals
( , , ) and ( ) and ( , , ).
Therefore, in this outside part, |x^2-3| = x^2-3 by the definition, and the original equation take the form
x^2 - 3 - 2x = 0. (3)
(Notice that it is DIFFERENT from equation (2)). Simplify and solve it
x^2 - 2x - 3 = 0 (3') ====> ).
Therefore, in this outside part, |x^2-3| = x^2-3 by the definition, and the original equation take the form
x^2 - 3 - 2x = 0. (3)
(Notice that it is DIFFERENT from equation (2)). Simplify and solve it
x^2 - 2x - 3 = 0 (3') ====>
 = = 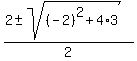 = = 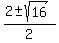 = = 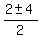 .
So, the equation (3') has two roots .
So, the equation (3') has two roots  = = 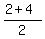 = 3 and = 3 and  = = 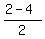 = -1.
Of these two roots, the root = -1.
Of these two roots, the root  = 3 lies out the interval ( = 3 lies out the interval ( , , )
THEREFORE, it is also the root of the original equation (1).
From the other side, the root )
THEREFORE, it is also the root of the original equation (1).
From the other side, the root  = -1 does belong to the interval ( = -1 does belong to the interval ( , , )
THEREFORE, it does not follow from our consideration that the root of )
THEREFORE, it does not follow from our consideration that the root of  = -1 is the root of the original equation (1).
Combining our results from n.1 and n.2, we conclude that the roots of the original equation (1) are 1 and 3.
4. Now it is good time to look into the plot and to see the big picture visually. = -1 is the root of the original equation (1).
Combining our results from n.1 and n.2, we conclude that the roots of the original equation (1) are 1 and 3.
4. Now it is good time to look into the plot and to see the big picture visually.
 Plot y = |x^2-3| - 2x
What you see in the figure, completely confirms my answer.
Plot y = |x^2-3| - 2x
What you see in the figure, completely confirms my answer.
The solution is completed.
------------------
In this site, there is a group of my lessons on solving Absolute Value equations
- Absolute Value equations
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 2
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 3
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 2
- OVERVIEW of lessons on Absolute Value equations
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and become an expert in this area.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Solving Absolute values equations".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13209)   (Show Source): (Show Source):
|
|
|