SOLUTION: Hi, Denise here. nice to meet you. I am studying algebra and am having problems with the algebraic word problems. I need help with. 1.) Joshua paid $26.50 for 10 gallons of ga

From the condition, you have these two equations


   10x + 2y = 26.50    (1)
    8x + 3y = 23.58    (2)


So, my equations and my variables are exactly as yours.


Now, if you try to apply the Substitution method directly as you learned it in the school, you will have denominators,

so, probably, you will not be happy. Therefore, let's try to use the Elimination method.


For it, multiply equation (1) by 3 (both sides), and multiply equation (2) by 2. You will get

    30x + 6y = 3*26.50    (3)
    16x + 6y = 2*23.58    (4)


Now subtract equation (4) from equation (3).  The terms " 6y " will cancel each other (it is how the Elimination method works)
and you will get

     30x - 16x = 3*26.50 - 2*23.58,   or

     14x = 32.34  =============>  x = 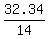 = 2.31.


Thus you found the price of one gallon of gas.


Now, in order for to find y, substitute the value x= 2.31  into either of the two equations (1) or (2).

I leave it to you to complete the solution on your own.