Question 1135433: 13. (18 pts) The cost, in dollars, for a company to produce x widgets is given by
C(x) = 4050 + 9.00x for x ≥ 0, and the price-demand function, in dollars per widget, is p(x) = 63-0.03x for 0 ≤ x ≤ 2100.
In Quiz 2, problem #10, it was seen that the profit function for this scenario isP(x) = -0.03x^2 + 54.00x-4050.
(a) The profit function is a quadratic function and so its graph is a parabola. Does the parabola open up or down? __________
(b) Find the vertex of the profit function P(x) using algebra. Show algebraic work.
(c) State the maximum profit and the number of widgets which yield that maximum profit:
The maximum profit is _____________, when ___________ widgets are produced and sold. (d) Determine the price to charge per widget in order to maximize profit.
(e) Find and interpret the break-even points. Show algebraic work.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The cost, in dollars, for a company to produce x widgets is given by
 for for  , and , and
the price-demand function, in dollars per widget, is
 for for
In Quiz 2, problem #10, it was seen that the profit function for this scenario is

(a) The profit function is a quadratic function and so its graph is a parabola. Does the parabola open up or down? ___ _______ _______
(b) Find the vertex of the profit function P(x) using algebra.

 ...complete square ...complete square

recall: 
since  , we have , we have  ...solve for ...solve for 

then we have



=> and and 
vertex is at: ( , ,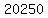 ) )
(c) State the maximum profit and the number of widgets which yield that maximum profit:
The maximum profit is _____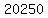 ________, when ___ ________, when ___ ________ widgets are produced and sold. ________ widgets are produced and sold.
(d) Determine the price to charge per widget in order to maximize profit.
 ...plug in ...plug in 



(e) Find and interpret the break-even points. Show algebraic work.
Break-Even _Point => when 
if


then 

 ...using quadratic formula we get: ...using quadratic formula we get:
 ≈ ≈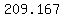
 ≈ ≈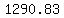
|
|
|