Question 1135367: if all permutations of the letters of the word AGAIN are arranged as in dictionary,then the 50th word is:
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
For solving such problems, there is beautiful Internet site
https://www.dcode.fr
which has a section devoted to permutations https://www.dcode.fr/permutations-generator.
It asked me what items I want to permute, and I pointed 5 letters A, G, A, I and N.
Then it asked me, if I want to have only DISTINGUISHABLE words as the output, and I answered "Yes".
In response, it generated 60 = 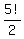 words placing them in column.
This output can be ordered in ascending or descending order - I selected "descending", exactly as in a dictionary
(it is also called lexicographic order).
From the list, I copied the 50-th line.
It is the word "NAAIG" , which is your ANSWER.
Probably, I could solve the problem without the help from this solver,
but in this case I decided to save my brain and my time.
Answer by greenestamps(13209)  (Show Source):
You can put this solution on YOUR website!
Given the usually excellent responses from tutor @ikleyn, I am CERTAIN she could have solved the problem without using the web site.
Given that the number of letters is relatively small, I would prefer to get the mental exercise....
(1) A _ _ _ _ : the remaining letters are AGIN; the number of permutations is 4! = 24
(2) G _ _ _ _ : the remaining letters are AAIN; the number of permutations is 4!/2! = 12; total number of permutations to this point = 24+12 = 36
(3) I _ _ _ _ : the remaining letters are AAGN; the number of permutations is 4!/2! = 12; total number of permutations to this point = 36+12 = 48
The 49th word is the first word that begins with N: NAAGI
The 50th word is the second word the begins with N: NAAIG
|
|
|
