Question 1135362: A particular fruit's weights are normally distributed, with a mean of 481 grams and a standard deviation of 9 grams.
If you pick 8 fruits at random, then 15% of the time, their mean weight will be greater than how many grams?
Give your answer to the nearest gram.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the mean of the population is 481 grams and the standard deviation of the population is 9 grams.
your sample size is 8.
therefore the standard deviation of the distribution of sample means, otherwise know as the standard error, is s = sdp / sqrt(ss).
s is the standard error
sdp is the standard deviation of the population
ss is the sample size.
s becomes equal to 9 / sqrt(8) = 3.181980515.
you need to look up the z-score for an area to the right of it being equal to .15.
this means you need to look up the z-score for an area of 1 - .15 = .85 to the left of it.
using the ti-84 plus calculator, i get a z-score with an area of .85 to the left of it equal to 1.03643338.
to find the raw score associated with this, use the z-score formula of z = (x - m) / s.
z is the z-score
x is the raw score.
m is the mean.
s is the standard error.
with a mean of 481 and a standard error of 3.181980515 and a z-score of 1.03643338, this formula becomes:
1.03643338 = (x - 481) / 3.181980515.
solve for x to get x = 1.03643338 * 3.181980515 + 481 = 484.2979108.
visually, this looks like this:
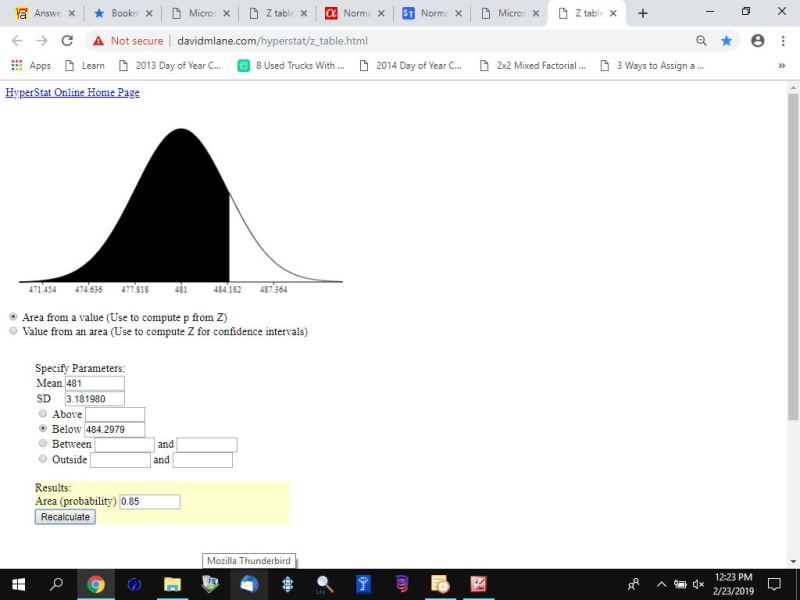
.85 area to the left of the value is equal to .15 area to the right of the value.
that looks like this.

your solution is that, if you pick a sample of 8 fruits at random, then 15% of the time their mean weight will be greater than 484.2979108 grams.
|
|
|