Question 113507: Example: Please help me solve this equation:  . .
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! solve this equation:  . .
----------------
The only possible rational roots are +1 and -1
But neither f(1) nor f(-1) is zero.
So, the equation has no rational solutions.
==============
Cheers,
Stan H.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Solution by Edwin
`
As Stanbon says, it has
no rational solutions, but
it can have irrational or
complex solutions,as we'll
see!!
Example: Please help me solve this equation:
 We try to see if we can factor that this
as the product of two quadratics:
(__x² + __x + __)(__x² + __ + __}
We know that
We try to see if we can factor that this
as the product of two quadratics:
(__x² + __x + __)(__x² + __ + __}
We know that  factors as factors as  times times  ,
so we choose 1's for the coefficients of x².
1 factors as either 1×1 or (-1)×(-1).
Since all the terms are positive we chose +1's to go in the
last blanks. So we try to see if we can find A and B such that
the left side factors this way: ,
so we choose 1's for the coefficients of x².
1 factors as either 1×1 or (-1)×(-1).
Since all the terms are positive we chose +1's to go in the
last blanks. So we try to see if we can find A and B such that
the left side factors this way:


 For this to be equivalent to the original equation, the
coefficients of like powers must be equal
Since the original equation is
For this to be equivalent to the original equation, the
coefficients of like powers must be equal
Since the original equation is
 we must have
we must have
 and and  , or , or  Solving the first for
Solving the first for  , ,  Sunstituting into
Sunstituting into 



 So
So  , and since , and since 
 So we have now factored te left side of
So we have now factored te left side of
 as
as
 We set each factor = 0, but since
the factors are the same, we only need
set one of them = 0:
We set each factor = 0, but since
the factors are the same, we only need
set one of them = 0:
 Solve that by the quadratic formula and get
x =
Solve that by the quadratic formula and get
x = 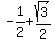  and x = and x = 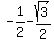  Each solution has multiplicity 2.
Edwin
Each solution has multiplicity 2.
Edwin
|
|
|