SOLUTION: The sum of the first five terms of an A.P is 36 and the sum of the next four terms is 90. find the A.P

Notice that from the condition, the sum of the first NINE terms is 36 + 90 = 126.


Now from the condition we have


      a)  the sum of the first 5 terms is  36,     (1) 
and
      b)  the sum of the first 9 terms is 126.     (2)


For any AP,  the sum of its first n terms is n times the arithmetic mean of the first and the n-th terms - 

therefore, for the given AP the arithmetic mean of the first and the 9-th terms is 126/9 =  14.


But in the given case this arithmetic mean of the first and the 9-th terms is nothing else as the 5-th term.


    Thus the 5-th term of the given AP is  14.



Similarly,  for the given AP the arithmetic mean of the first and the 5-th terms is 36/5 =  7.2.

But in this case this arithmetic mean of the first and the 5-th terms is nothing else as the 3-rd term.


    Thus the 3-rd term of the given AP is  7.2.


Between the 3-rd and the 5-th terms there are two equal gaps, each equal to the common difference.


So, the common difference of the given AP is 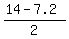  = 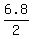 = 3.4.



Now we know that the 3-rd term of the AP is 7.2 and the common difference is 3.4.

Hence, its 1-st term is  7.2 - 2*3.4 = 7.2 - 6.8 = 0.4.


Now we know ALL about this AP:   = 0.4  and  d = 3.4.       ANSWER


CHECK

n       
----------------

1	0.4		
2	3.8		
3	7.2		
4	10.6		
5	14	sum from 1 to 5 = 	36       ! Correct !
6	17.4		
7	20.8		
8	24.2		
9	27.6	sum from 1 to 9 = 	126      ! Correct !