Question 1134745: A square graphed on the coordinate plane has a diagonal with endpoints E(2, 3) and F(0, -3).
What are the coordinates of the endpoints of the other diagonal?
A, (4,−1) and (−3,−1)
B. (4,−1) and (−2,1)
C. (4,0) and (−2,−1)
D. (3,−1) and (−2,−1)
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the answer is selection B.
there are probably many ways to derive the solution, but the method i chose is as follows:
the diagonal is the line between (2,3) and (0,-3).
if you circumscribe the square with a circle, then the center of that circle will be at the midpoint of this line.
the midpoint of this line is equal to the coordinate point of (1,0).
since the diagonals of squares are perpendicular to each other, then the other diagonal will be a line through the point (1,0) and perpendicular to the line going through the points (2,3) and (0,-3).
the line going through the points (2,3) and (0,-3) is formed from the equation of y = 3x - 3.
the other line will be perpendiular to this line and go through the point (1,0).
the equation of that line is y = -1/3 * x + 1/3.
i did not show you how to derive the equation of these lines because i'm assuming you already know how to do so.
i also assumed you know how to find the midpoint of a line.
if you don't, let me know and i'll show you how i did it.
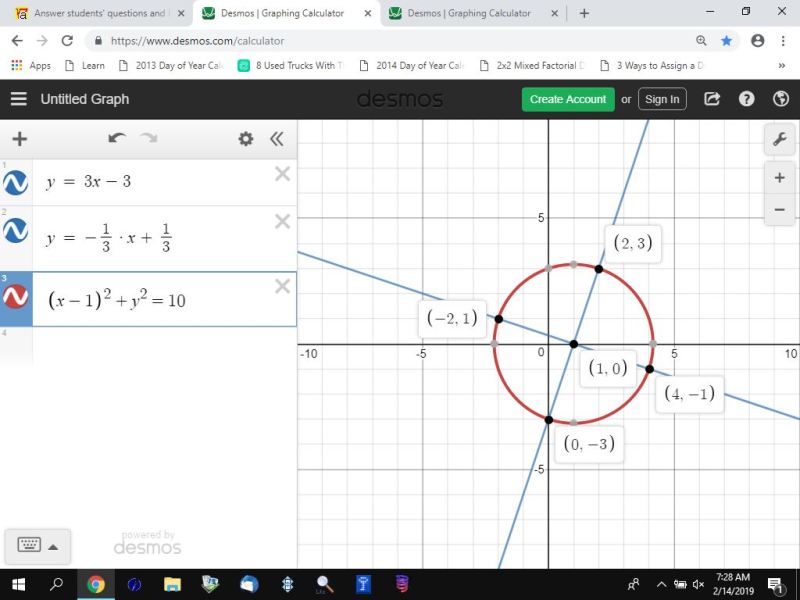
the circle that is circumscribed around the square has its center at (1,0).
the equation for this circle is (x-1)^2 + y^2 = 10.
once again, i'm assuming you know how to derive the equation of a circle with a center at (1,0).
again, if you don't know how to do that, let me know and i will show you how i did it.
i then used graphing software at desmos.com/calculator to find the intersection points of the diagonals with this circle.
those intersection points are:
(0,-3) and (2,3) for the original diagonal.
(-2,1) and (4,-1) for the other diagonal.
connect the corner points of each of these diagonals to each other and you have your square.
you would connect:
(-2,1) to (2,3)
(2,3) to (4,-1)
(4,-1) to (0,-3)
(0,-3) to (-2,1)
as i said before, there may be other ways to do it, but this way seemed to be simple enough, assuming you know how to get the equations of the required lines and circle.
the graphing software makes finding the intersection points easy.
if not for that, you would have needed to create simultaneous equations and then solve for the common points.
for example:
the equation of the circle is (x-1)^2 + y^2 = 10
the equation of one of the diagonals is y = 3x - 3.
replace y in the first equation with 3x - 3 from the second equation to get first equation = (x-1)^2 + (3x-3)^2 = 10
simplify to get x^2 - 2x + 1 + 9x^2 - 18x + 9 = 10
combine like terms to get 10x^2 - 20x + 10 = 10
subtract 10 from both sides of this equation to get 10x^2 - 20x = 0
divide both sides of this equation by 10 to get x^2 - 2x = 0
factor out the x to get x * (x-2) = 0
solve for x to get x = 0 or x = 2.
go back to your first equation of y = 3x - 3 and replace x with 0 to get y = -3.
go back to your first equation of y = 3x - 3 again and replace x with 2 to get y = 6 - 3 which results in y = 3.
when x = 0, y = -3 give you the coordinate point of (0,-3) where the circle intersects with the original diagonal line.
when x = 2, y = 3 gives you the coordinate point of (2,3) where the circle intersects with the original diagonal line.
you do the same procedure with the other diagonal line and will get the other intersection points shown on the graph.
once again, if there are any parts of this that you don't understand how to do, let me know and i'll take you through them.
the graphing software i used is at desmos.com/calculator.
here's my graph with the intersection shown.
Answer by ikleyn(52813)   (Show Source): (Show Source):
|
|
|