SOLUTION: Write the slope intercept form of the equation of the described line: Through (-3,-5) and perpendicular to x+2y=-4 Helppppp!!!! :(

Click here to see ALL problems on Linear-equations

Question 1134741: Write the slope intercept form of the equation of the described line:
Through (-3,-5) and perpendicular to x+2y=-4
Helppppp!!!! :(
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website!
-----------------------------------------------
Through (-3,-5) and perpendicular to x+2y=-4
-----------------------------------------------

Slope of your given line is .
Slope for any line perpendicular to given line must be , which is negative reciprocal of .

Starting with point-slope form:

-

-------finished in slope-intercept form

Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website!
.

            It is VERY EASY.

The given line x + 2y = -4 has the slope m = . You MOMENTARILY find it (the slope) by transforming the given equation to the form y = 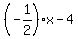. Next, the perpendicular line has the slope, which is reciprocal opposite to , i.e. 2. Thus the perpendicular line has the form y = 2x + c. (1) The constant term "c" in this equation is now UNKNOWN, but we momentarily will find it using the condition that the given point (-3,-5) lies on the line (1). For it, substitute coordinates x= -3 and y= -5 into equation (1). You will get -5 = 2*(-3) + c, which gives you c = - 5 + 6 = 1. So, your final equation is y = 2x + 1. ANSWER

Solved.

-------------------

For this and many other similar problems see the lessons
    - Find the slope of a straight line in a coordinate plane passing through two given points
    - Equation for a straight line having a given slope and passing through a given point
    - Solving problems related to the slope of a straight line
    - Equation for a straight line in a coordinate plane passing through two given points
    - Equation for a straight line parallel to a given line and passing through a given point
    - Equation for a straight line perpendicular to a given line and passing through a given point (*)
in this site.

The most relevant of them is the lesson marked (*) in the list.

Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.

Answer by greenestamps(13209)   (Show Source):
You can put this solution on YOUR website!

You have received two good solutions to your problem that use similar basic algebraic techniques, utilizing the fact that the slopes of perpendicular lines (except horizontal and vertical lines) have slopes that are negative reciprocals.

There is a shortcut to solving this kind of problem.

(If the equation doesn't have to be in slope-intercept form, this shortcut gets you to AN equation of the line immediately; in this problem, since an equation in slope-intercept form is required, the shortcut doesn't save much time.)

Given a line with equation Ax+By=C, any line parallel to that given line has an equation of the form Ax+By=D (where D is some probably different constant); and any line PERPENDICULAR to that given line has an equation of the form Bx-Ay=E (where again E is some constant).

Note the coefficients are switched; and one of them changes sign.

In your example, the given line has the equation x+2y=-4. Any line perpendicular to that line has an equation of the form 2x-y=C.

Plug in the coordinates of the given point the find C; then convert the equation to slope-intercept form.

, so the equation is