SOLUTION: x^(1/2) - x^(1/4) - 2 = 0, find x.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: x^(1/2) - x^(1/4) - 2 = 0, find x.       Log On


   

Question 1134459: x^(1/2) - x^(1/4) - 2 = 0, find x.
Found 2 solutions by ikleyn, t0hierry:
Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.
The domain of this equation is  x >= 0,  x^(1/2) >= 0  and  x^(1/4) >= 0.


Introduce new variable  y = x^(1/4).


Then the equation takes the form


    y^2 - y - 2 = 0


Factor left side


    (y-2)*(y+1) = 0.


The roots are  y= 2  and  y= -1.


Case (a).  y= 2  ====>  x^(1/4) = 2  ====>  x = 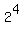2%5E4 = 16.


Case (b).  y= -1  ====  x^(1/4) = -1  ====> It is out of the domain, so it does not lead to any solution for x.

Solved and answered.

----------------------

There are two lessons to learn from my post. 

    1.  Before solving such an equation, establish the domain, i.e. the set of possible (and impossible) solutions.


    2.  Introducing new variable is the STANDARD method of solving such equations.


Answer by t0hierry(194) About Me  (Show Source):
You can put this solution on YOUR website!
y = x^1/4
y^2 = x^1/2
y^2 - y - 2 = 0
You can solve or y or "see" that
y = -1
y = 2
Then go back to x
y = 2 gives you y^4 = 16 = x
y = -1 gives you a complex number
x^2 = i, x = cos(pi/4) + i sin(pi/4);
x^2 = -i, x = cos(-pi/4) + i sin(-pi/4)