Question 1134388: The oranges produced by an orchard are packed in boxes. Each box contains 60 oranges. On the average, 2% of the oranges are rotten when they arrive at a fruit shop. By using a suitable approximation, calculate the probabilty that in a box which contains 60 oranges, there are:
1) no rotten oranges
2) at least 3 rotten oranges
3) if a fruit shop orders 100 boxes of oranges, find the probabilty that exactly 2 boxes contain at least 3 rotten oranges
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if 2% of the oranges in a box are rotten on average, then the probability that an orange in the box is rotten is .02.
the probability that an orange in the box is not rotten would therefore be 1 - .02 = .98.
this appears to be a binomial probability type of problem.
the formula for that is p(x) = p^x * q^(n-x) * c(n,x)
p = .02
q = .98
c(n,x) = n! / (x! * (n-x)!)
n = 60
x = number of rotten oranges in the box.
based on that formula, probability of 0 rotten oranges is 0.297553143.
based on that formula, probability of at least 3 rotten oranges is 1 minus p(0) + p(1) + p(2) rotten oranges in the box.
that would be equal to 1 minus 0.881257975 equals 0.118742025.
if a fruit shop orders 100 boxes, the probability that there will be exactly 2 boxes that contain at least 3 rotten oranges would be calculated as follows.
the probability that any one box chosen at random contains 3 or more rotten oranges is 0.118742025.
100 boxes were purchased, therefore the new n = 100
the new p is .118742025.
the new q is equal to 1 - p which is equal to 0.881257975
x is equal to 2.
p(x) = p^x * q^(n-x) * c(100,2) = .0002910140787.
this is what i think should be your solution.
it makes use of the binomial probability formula of p(x) = p^x * q^(n-x) * c(n,x).
here's a reference on that formula.
https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/binomial-theorem/binomial-distribution-formula/
here's a display of my use of excel to perform the calculations required.
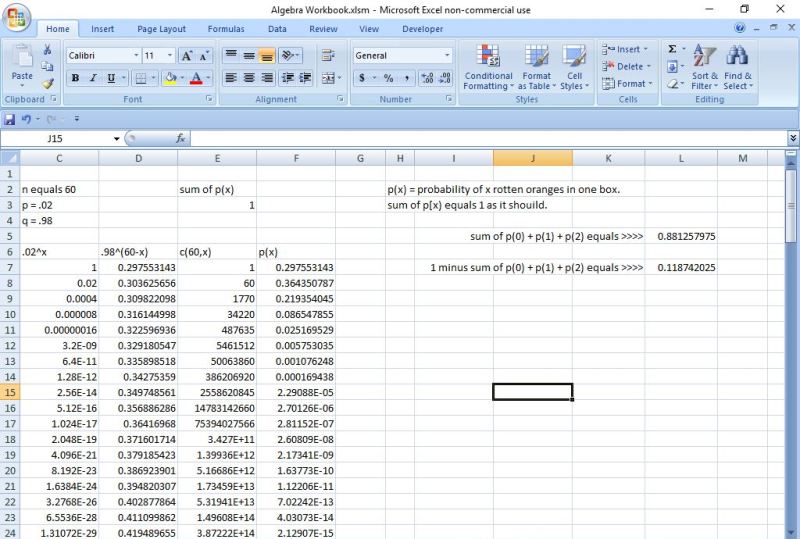
the use of the binomial probability formula is based on my assumption that:
an orange in a box is either rotten or it's not.
the probability of an orange in a box being rotten is independent of the probability of another orange in that same box being rotten.
a box either contains 3 or more rotten oranges or not.
the probability of one box containing 3 or more rotten oranges is independent of another box containing 3 or more rotten oranges.
the debatable portion of these assumptions is the probability of an orange in a box being rotten being independent of the probability of another orange in that same box being rotten.
i chose to ignore the fact that one rotten orange in a box may in fact have an impact on the probability of another orange in the box being rotten.
my reasoning is that the oranges in the box are probably not in the box long enough for this to happen.
that reasoning is a simplifying assumption to allow for the use of the binomial probability formula.
without that simplifying assumption, i'm not exactly sure what formula you could use because the formula requires that the probability of the event happening is independent of any other event happening.
|
|
|