Question 1134236: Hi! Looking at my teachers notes, they do not make sense. I am also waiting on an emai from her for extra help, but I figure ask here as well since I’ve gotten help before and it does help reading this and asking my teacher. The question is:
A class of 28 students took a 100 point test. If the mean was 68, is it possible that 23 of the students got a score of 63 or lower?
Thank you!
Found 4 solutions by Glaviolette, jim_thompson5910, rothauserc, ikleyn:
Answer by Glaviolette(140)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since the mean is 68, that means the sum of the scores would be 28*68 = 1904. Let's use the maximum value allowed of 63. If 23 scores were 63, 23*63 = 1449. Subtracting that from 1904 leaves 455 "points" to be scored among the remaining 5 students. This works out to an average of 91 points per student, so yes it is possible.
Those 23 scores wouldn't be able to be much lower than 63. The remaining 5 students could get a max of 100 points each, for a total of 500 points. So that would leave 1904-500=1404 for the 23 students. 1404/23 is about 61 points per student.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Yes it is possible, and here's why:
Focus on the phrase " 23 of the students got a score of 63 or lower". Let's assume that all 23 students got the same score of 63, which is the highest possible for this group. This would mean that the total sum of the scores so far is 23*63 = 1449. Basically if you had 23 copies of "63" added up, you'd get to 1449.
Add on 5*x which represents the idea of having 5 other students score some other value x. Keep in mind that x is in the interval from 0 to 100. Anything outside this interval does not make sense. You can't get a negative score. You cannot get a score over 100 (assume there's no extra credit)
So we add 5x to 1449 to get 5x+1449. This total sum is divided over the number of students, which is 28, to get this expression 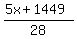 . This expression represents the average of all 28 students. The first 23 scored a 63, while the other 5 got a score of 'x' (to be determined) . This expression represents the average of all 28 students. The first 23 scored a 63, while the other 5 got a score of 'x' (to be determined)
Set this expression equal to the target average we want, which is 68. Let's solve for x

 Multiply both sides by 28 Multiply both sides by 28

 Subtract 1449 from both sides Subtract 1449 from both sides

 Divide both sides by 5 Divide both sides by 5

Therefore, the other five students must score 91 on each test so that the entire class averages a 68.
So it is possible, and I'm sure there are other scenarios where you can have the class average a 68 even if you don't have two groups scoring the same. Though of course, if the first group has too low of scores then at some point the other group won't have enough to bring up the overall average.
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! 28 * 68 = 1904 total points
:
23 * 63 = 1449 points
:
1904 - 1449 = 455 points for 5 students to make up
:
455/5 = 91
:
It is possible, if all 23 students scored 63 and the remaining 5 students scored 91.
:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If the class of 28 students took a 100 point test and if the mean was 68, then the total points was 28*68 = 1904.
Let assume that for some 23 students their average score was 63 or lower - then the total score for these 23 students was 23*63 = 1449 or lower.
Hence, the difference is 1904 - 1449 = 455 or greater, and it is what the rest of 28-23 = 5 students get altogether.
Since 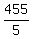 = 91 is less than 100, there is NO CONTRADICTION, which means that the given outcome IS POSSIBLE. = 91 is less than 100, there is NO CONTRADICTION, which means that the given outcome IS POSSIBLE.
---------------
Usually, the problems of this kind are designed to get a contradiction and thus disprove the possibility.
But in the given / (posted) case, this hypothetical design / ("solution strategy") does not work.
INTERESTING NOTICE / addition.
If, on the contrary, I slightly change the problem formulation in this way
A class of 28 students took a 90 point test. If the mean was 68, is it possible that 23 of the students got a score of 63 or lower?
then the answer is "IT IS IMPOSSIBLE", and the proof is as follows:
If the class of 28 students took a 90 point test and if the mean was 68, then the total points was 28*68 = 1904.
Let assume that for some 23 students their average score was 63 or lower - then the total score for these 23 students was 23*63 = 1449 or lower.
Hence, the difference is 1904 - 1449 = 455 or greater, and it is what the rest of 28-23 = 5 students get altogether.
But 90*5 = 450 is LESS than 455, so in the 90-point test 5 students CAN NOT obtain 455 points cumulatively.
CONTRADICTION (!).
Which proves that IT IS IMPOSSIBLE (!)
Hope my explanations make the general picture more clear to you . . .
|
|
|